[科普中国]-第六类例外典型域

第六类例外典型域(exceptional classical do-main of sixth class)是典型域之一。典型域是多复变函数论的基本概念。Cn中不可分解对称有界域在全纯等价下分类的标准域称为典型域。

概念第六类例外典型域(exceptional classical do-main of sixth class)是典型域之一。第六类例外典型域RⅥ(27)：它双全纯同构于无界域：

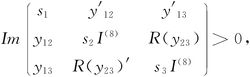
其中s1，s2，s3∈C，y12，y13，y23∈C，记：

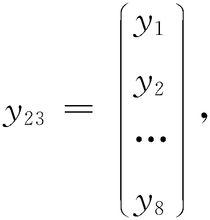
则

R(y23)=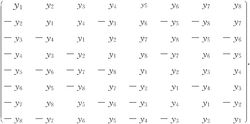

第五类例外典型域第五类例外典型域(exceptional classical do-main of fifth class)是典型域之一。第五类例外典型域Rv(16)：它双全纯同构于无界域：

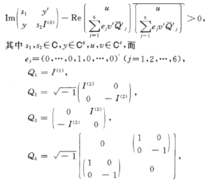
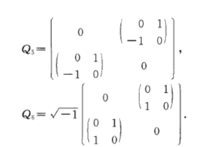
第四类典型域第四类典型域(classical domain of fourthclass)亦称李球，典型域之一。第四类典型域：

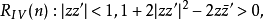其中z=(z1，z2，…，zn)为由n个独立复变量z1，z2，…，zn构成的1×n矩阵。

第三类典型域第三类典型域(classical domain of third class)是典型域之一。第三类典型域：

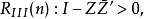其中Z′=-Z，即Z由n(n-1)/2个独立变量：

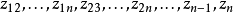构成，又：

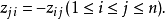
典型域典型域是多复变函数论的基本概念。Cn中不可分解对称有界域在全纯等价下分类的标准域称为典型域。它们有四大类和两个特殊的域，分别在16维及27维复欧氏空间中，这两个域也称为例外典型域。1

多复变函数论多复变函数论是研究多个复变量的全纯函数的性质和结构的学科，是分析学的一个分支，有时也称之为多复分析。

多复变函数论的研究，早在单复变函数论的黎曼和外尔斯特拉斯时代就已经零散地开始了。但真正标志着多复变函数论这一学科创立的，是19世纪末和20世纪初庞加莱、库辛和哈托格斯等人的工作。他们的工作揭示了多复变全纯函数本质上的独特性。在这当中，库辛提出的关于全纯函数整体性质的两个以他的名字命名的问题以及列维提出的拟凸域和全纯域是否等价的问题，更有着深远的影响，长时间成为多复变函数论发展的推动因素。20世纪30年代以前，虽然出现过莱因哈特关于解析自同构群、伯格曼关于核函数和度量等方面的重要工作，但整体说来，多复变函数论处于相对沉寂时期。从20世纪30年代开始，多复变函数的研究迎来了初步繁荣。在这一时期陆续出现了H.嘉当关于全纯自同构的唯一性定理、有界域全纯自同构群的李群性质以及全纯域与全纯凸的等价性的嘉当—苏伦定理等突出成果。特别是从1936年开始，日本数学家冈洁对库辛问题、列维问题、逼近问题等多复变的中心问题进行了长期、系统而富有成效的研究，终于在20世纪50年代对上述诸问题给出了解答。他的这一系列工作对后来多复变函数的发展有着重大影响。20世纪50年代以后，和现代数学的综合化、抽象化的总潮流相一致，在多复变函数论中用拓扑方法和几何方法研究全纯函数的整体性质的趋势变得越来越明显。由勒雷引进拓扑学的层及其上同调的概念被迅速而成功地用于多复变函数。这一概念和H.嘉当早先关于全纯函数理想论的研究以及冈洁的思想结合，导致了凝聚解析层理论的建立。与此同时，复空间与施泰因流形的概念也应运而生。H.嘉当和塞尔系统地应用凝聚层理论建立了施泰因流形的基本定理。此后不久，格劳尔特解决了复流形的列维问题，他和雷默特、施泰因等人还大大发展了复空间的理论。整个20世纪50年代是多复变函数的黄金时代。

另一方面，近代微分几何与复分析的相互融合也在不断地加快步伐。1913年，外尔的黎曼曲面理论导致了复流形概念的建立。E.嘉当的外微分式与拓扑的结合产生了德·拉姆的上同调理论。以此为基础，霍奇将黎曼曲面上的调和函数理论推广到高维的紧致复流形，证明了紧复流形的基本定理——霍奇定理。20世纪40年代以后，与微分几何中的博赫纳技巧相结合，霍奇理论又由小平邦彦所发展和完善。20世纪60年代，博赫纳—小平邦彦方法又进而推广到非紧的带边界的复流形，发展成为近代多复分析的一个有力工具——问题的L估计。

多复变函数论中具有重要意义的第三方面进展是西格尔在1935——1950年间建立的多复变函数的自守函数论。20世纪50年代以后，由于塞尔伯格、朗兰茨、盖尔范德等人的工作，揭示了它与代数数论、李群的无穷维表示、代数几何等众多学科的内在联系，而日益成为目前极为活跃而且引人注目的近代数学领域之一。1

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院