[科普中国]-卡拉西奥多里伪距

卡拉西奥多里伪距是距离的定义方式之一。在数学中，距离是泛函分析中最基本的概念之一。

简介卡拉西奥多里伪距是距离的定义方式之一。

复流形M到单位圆盘B内的全体全纯映射构成集合B(M)，则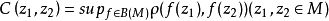 称为卡拉西奥多里伪距，其中ρ为M的庞加莱度量导出的距离。1

全纯映射全纯映射是复流形上的一种有解析性的映射。

设M，N分别是复m，n维复流形，f：M→N是连续映射。若对每一点p∈M，存在一个邻域U，使得f在U内可用局部坐标函数表示成：

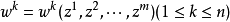
其中ω都是全纯函数，则称f是全纯映射。

距离在数学中，距离是泛函分析中最基本的概念之一。它所定义的距离空间连接了拓扑空间与赋范线性空间等其他空间，是学习泛函分析首先接触的概念。

设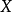是任一非空集，对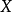中任意两点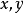有一实数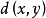与之对应且满足：
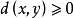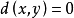1)非负性、同一性：，且当且仅当；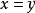
2)对称性：；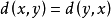
3)直递性：。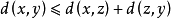
称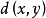为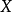中的一个距离，定义了距离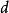的集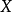称为一个距离空间，记为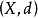，在不引起混乱的情形下简记为。

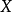本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院