[科普中国]-伯格曼核函数

伯格曼核函数是刻画有界域函数论性质和几何性质的一个极有用的正值函数。

简介伯格曼核函数是刻画有界域函数论性质和几何性质的一个极有用的正值函数。

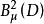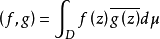设D为Cn中的有界域，记μ为Cn的欧几里得测度，考虑函数空间其中Hol(D)为D上所有全纯函数构成的集合，在中引进内积于是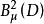关于此内积为希尔伯特空间，且有可数积。任给完备规范正交基φ1,φ2,...，于是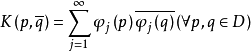关于p及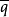为全纯函数，且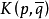与规范正交基的选取无关。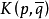称为有界域D上的伯格曼核函数。1

性质平方可积全纯函数f(z)可表为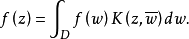

全纯函数全纯函数是复理论研究的核心之一，它们是复流形到 C 的处处可微函数。全纯比实可微强很多，它直接推出函数无穷阶可微并可泰勒展开。“(复)解析函数(analytic function)” 可和 “全纯函数” 交换使用，但不常用，一般用来指实解析函数。

"在一点全纯" 可推出在该点的某个开邻域可微。类似地，可以定义全纯多复变函数。全纯映射(holomorphic mapping) 是指两个复流形之间的局部全纯函数。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院