[科普中国]-逆变换采样

逆变换采样（英语：inverse transform sampling），又称为逆采样（inversion sampling）、逆概率积分变换（inverse probability integral transform）、逆变换法（inverse transformation method）、斯米尔诺夫变换（Smirnov transform）、黄金法则（golden rule）等，是伪随机数采样的一种基本方法。在已知任意概率分布的累积分布函数时，可用于从该分布中生成随机样本。

简介逆变换采样（英语：inverse transform sampling），又称为逆采样（inversion sampling）、逆概率积分变换（inverse probability integral transform）、逆变换法（inverse transformation method）、斯米尔诺夫变换（Smirnov transform）、黄金法则（golden rule）等，1是伪随机数采样的一种基本方法。在已知任意概率分布的累积分布函数时，可用于从该分布中生成随机样本。

定义假设X为一个连续随机变量，其累积分布函数为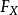。此时，随机变量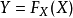服从区间[0,1]上的均匀分布。逆变换采样即是将该过程反过来进行：首先对于随机变量 Y，我们从0至1中随机均匀抽取一个数u。之后，由于随机变量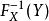与X有着相同的分布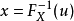，即可看作是从分布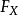中生成的随机样本。

示例假设有一个累积分布函数

我们要从该分布中生成随机样本。F(x)的反函数为：

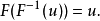
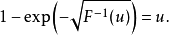
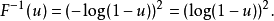于是，我们先从0至1中随机均匀抽取 u，然后计算以得到我们需要的样本。

本词条内容贡献者为:

于仁业 - 高级工程师 - 中航工业哈尔滨飞机工业集团有限责任公司