[科普中国]-多卷波混沌吸引子

多卷波混沌吸引子(N scroll chaotic attractor)也称N卷波吸引子在保密数码通讯，同步预测等方面有重要应用。

超混沌陈氏吸引子陈氏系统：1

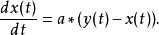
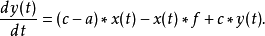
其中 f 为调控函数：1

正弦调控函数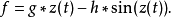

参数：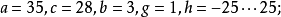

初始条件：

initv := x(0) = 1, y(0) = 1, z(0) = 14；

利用龙格－库塔-菲尔伯格法（Runge–Kutta–Fehlberg，简称 RKF45）可得数字解并做图。

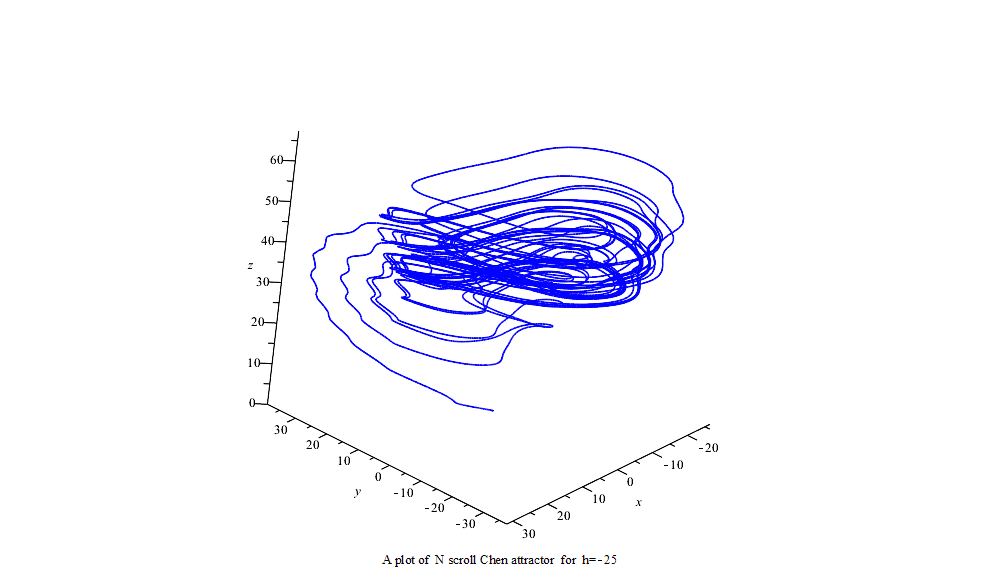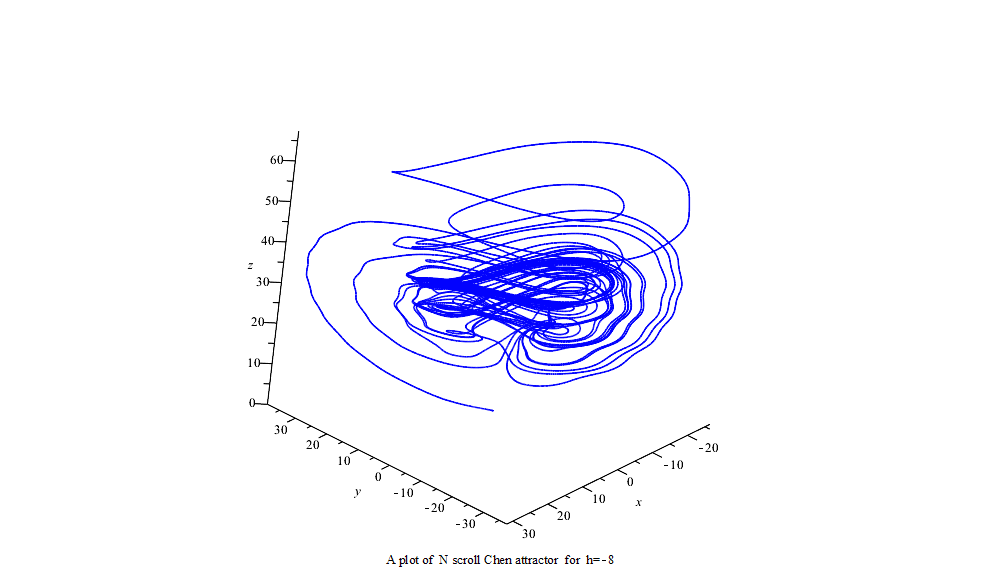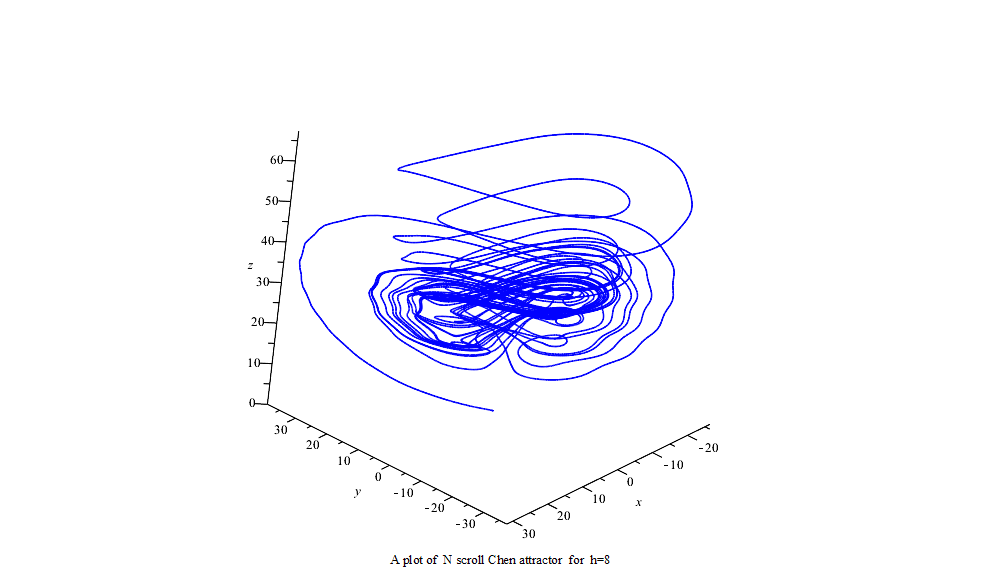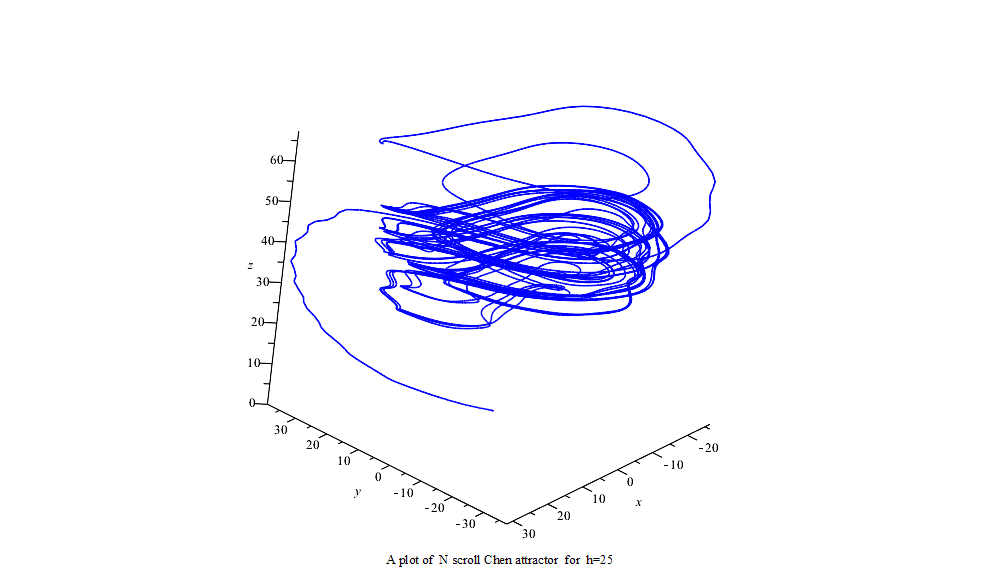
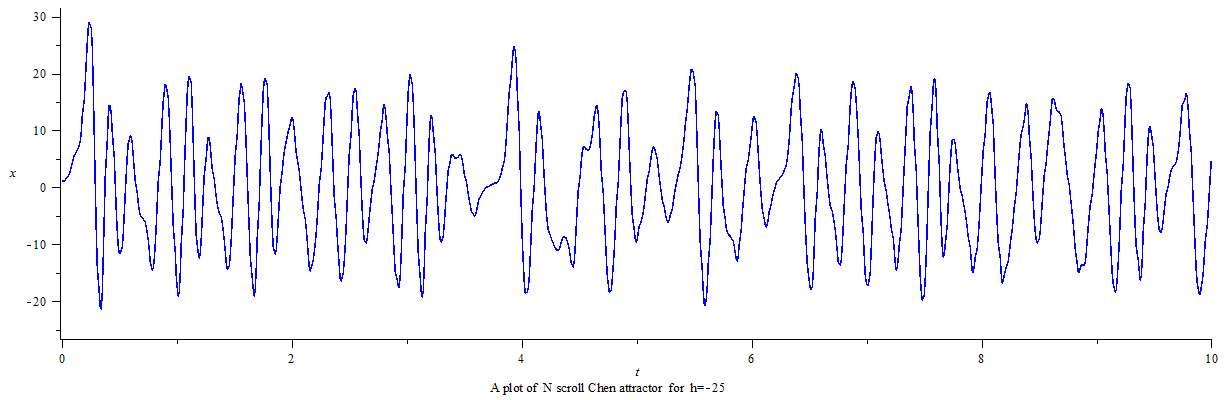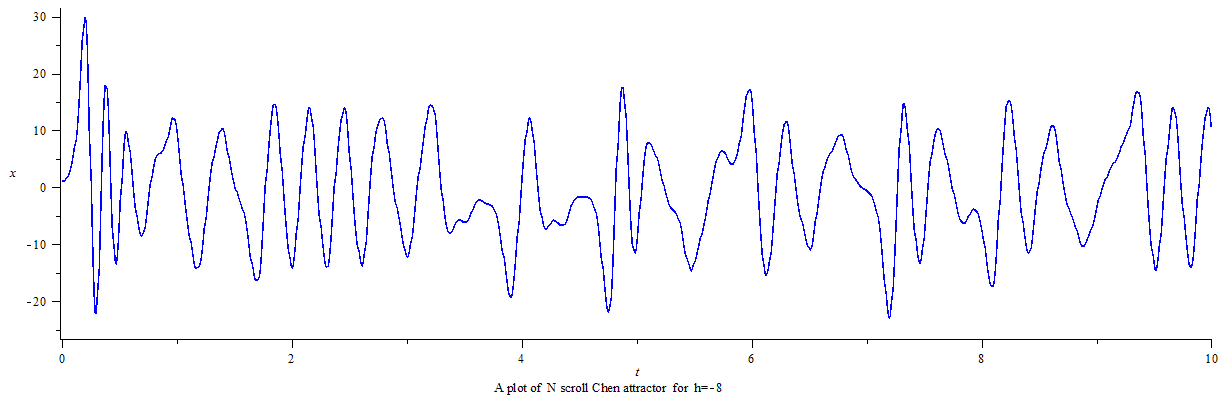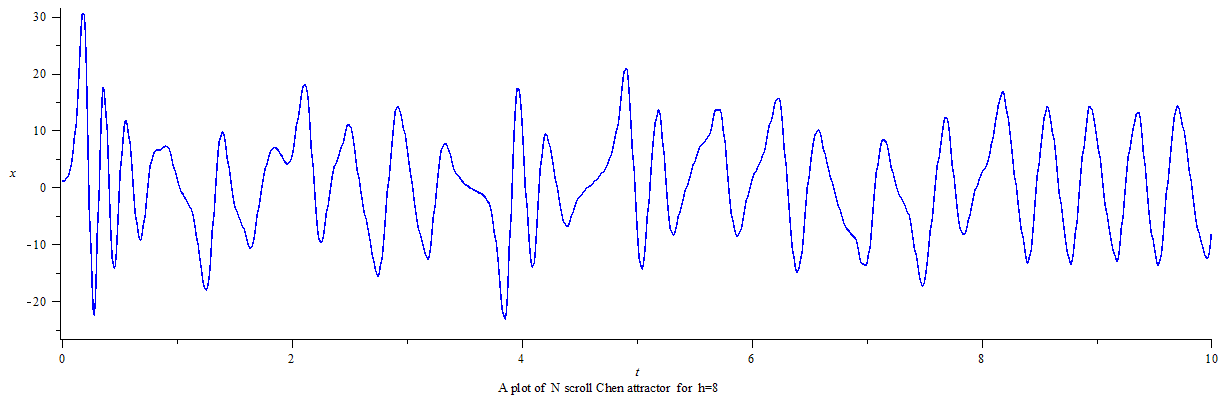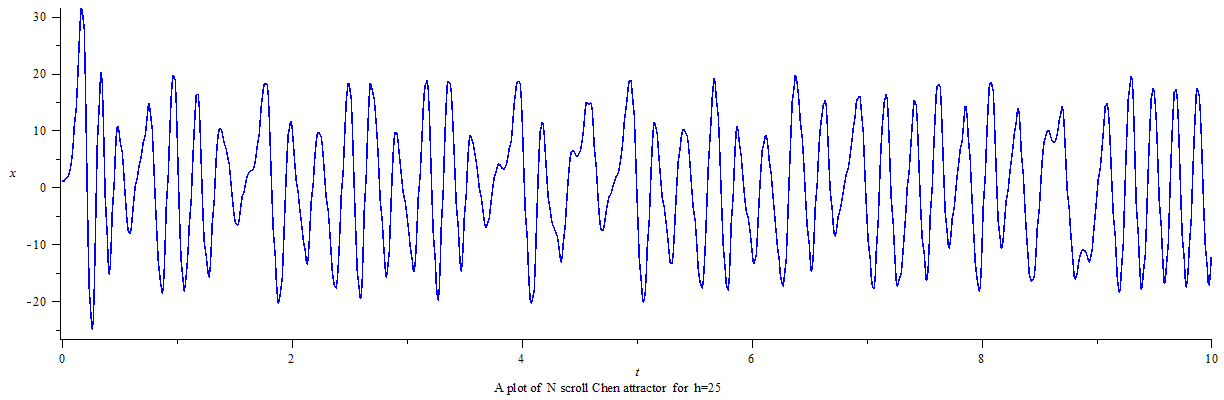
延时正弦函数

参数 params:= a = 35, c = 28, b = 3, d0 = 1, d1 = 1, d2 = -20..20, tau = .2

初始条件 initv:= x(0) = 1, y(0) = 1, z(0) = 14。

利用龙格－库塔-菲尔伯格法（Runge–Kutta–Fehlberg法，简称 RKF45）可得数字解并做图

延时正弦函数多卷波广义陈氏吸引子

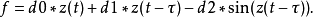
参数 params := a = 35, c = 28, b = 3, d0 = 1, d1 = 1, d2 = -20..20, tau = .2

初始条件 initv := x(0) = 1, y(0) = 1, z(0) = 142

利用龙格－库塔-菲尔伯格法（Runge–Kutta–Fehlberg法，简称 RKF45）可得数字解并做图。

超混沌蔡氏吸引子2001年Tang等提出改进的蔡氏吸引子系统：2.

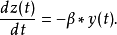
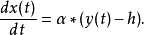
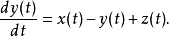
其中

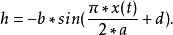
参数 params := alpha = 10.82, beta = 14.286, a = 1.3, b = 0.11, c = 7, d = 0

初始条件 initv := x(0) = 1, y(0) = 1, z(0) = 0

龙格－库塔-菲尔伯格法获得数字解并做图：

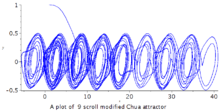
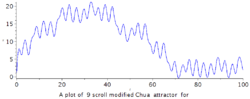
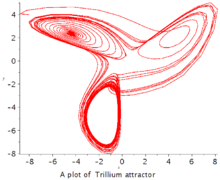
延龄草型混沌吸引子1993年 Miranda & Stone 提出下列方程组：2

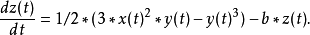
参数： a = 10, b = 8/3, c = 137/5；

初始条件： x(0) = -8, y(0) = 4, z(0) = 10；

利用龙格－库塔-菲尔伯格法（Runge–Kutta–Fehlberg法，简称 RKF45）可得数字解并做图。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学