[科普中国]-赋可列范线性空间

设E是局部凸空间，如果E的拓扑可由可列个连续范数{pn(∙)}确定，则称E是赋可列范线性空间。

简介赋可列半范线性空间是一类局部凸空间。

设E是局部凸空间，如果E的拓扑可由可列个连续半范数{pn(∙)}确定，则称E是赋可列半范线性空间。不失一般性，还可以要求p1(x)≤p2(x)≤...≤pn(x)≤...(x∈E)。当pn都是范数时，称E为赋可列范线性空间。1

范数范数(norm)是数学中的一种基本概念。在泛函分析中，它定义在赋范线性空间中，并满足一定的条件，即①非负性；②齐次性；③三角不等式。它常常被用来度量某个向量空间（或矩阵）中的每个向量的长度或大小。

范数是具有“长度”概念的函数。在线性代数、泛函分析及相关的数学领域，范数是一个函数，是矢量空间内的所有矢量赋予非零的正长度或大小。半范数可以为非零的矢量赋予零长度。

定义范数的矢量空间是赋范矢量空间；同样，定义半范数的矢量空间就是赋半范矢量空间。

赋范线性空间(normed linear space)

赋范线性空间是在线性空间中引进一种与代数运算相联系的度量，即由向量范数诱导出的度量。赋范线性空间称为Banach空间，是指由范数导出的度量是完备的。

定义：设是线性空间，函数称为上定义的一个范数，如果满足：

（1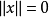）当且仅当；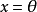

（2）对任何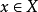及，；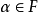

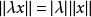（3）对任意，。

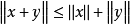称二元体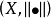为赋范线性空间。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学