[科普中国]-哈托格斯定理

哈托格斯定理是给出多复变函数成为全纯函数所需的最弱条件的命题。哈托格斯花了很大的力气才证明：多复变函数全纯当且仅当它对每个自变量都是全纯的。

定义哈托格斯定理是给出多复变函数成为全纯函数所需的最弱条件的命题。

设n≥2，D是Cn中的域，f=f(z1,z2,...,zn)是D上的单值函数。哈托格斯定理定理断言：如果对于任意j(1≤j≤n)和任意一点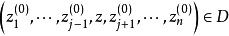 ，单复变函数 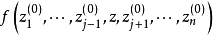在点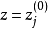 全纯，则f在D上为全纯函数。1

推论复平面上任何单连通的开集上都存在一个单复变函数，它不能延拓到这个开集之外--满足这种性质的开集叫做全纯域。但是在多复变函数里却发生了奇特的现象：有一些开邻域，它们上面的任何全纯函数都可以延拓到外面去。这种现象称为哈托格斯现象。 如果一个开邻域不能发生哈托格斯现象，我们就成这个邻域为全纯域。

哈托格斯花了很大的力气才证明：多复变函数全纯当且仅当它对每个自变量都是全纯的。 这个结论看似简单，实则难矣。迄今为止，人们都没有找到一个简化的证明。

相关概念多复变函数自从复变函数的理论被广泛应用于数学的各个分支后，人们自然想把复分析推广到任何多个自变量，以及任何多个因变量的复向量值函数上。多复变函数就是研究这类推广的复变函数。

全纯函数全纯函数是复理论研究的核心之一，它们是复流形到 C 的处处可微函数。

设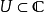开子集且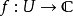是一个单复变函数，称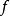在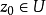(复)可微或全纯，如果极限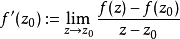存在。

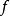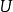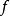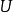若在中处处可微，则称在上全纯。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学