[科普中国]-文本信息检索技术

文本信息检索是针对文本的信息检索技术。在技术社区中，文本信息检索常常被等同于信息检索技术本身。

相对视频、音频检索而言，文本信息检索是发展较快也较成熟的，其他模态的信息检索技术，往往也要仰赖文本信息检索的支持。

虽然网络搜索引擎目前已不仅仅局限于对文本进行检索，文本信息检索仍然是大部分网络搜索引擎的基础。

历史介绍自人类的文字产生起，如何快速地从大量的，记录在各种各样的存储媒体中查找或获取信息就成为一个引人注目的问题。这个问题关系到人类如何能够主动地获取自己需要的知识。因此，文本信息检索技术甚至可以追述到古代的书籍编目。但是直到近一个世纪，随着人类的知识以前所未有的速度急剧膨胀，信息存储方式越来越丰富，使得在海量的，多模态的信息库中进行快速、准确的检索成为急迫的需求。1945年，Vannevar Bush的论文《就像我们可能会想的……》1第一次提出了设计自动的，在大规模的存储数据中进行查找的机器的构想。这被认为是现在信息检索技术的开山之作。进入50年代后，研究者们开始为逐步的实现这些设想而努力。在50年代中期，在利用计算机对文本数据进行检索的研究上，研究者获取了一些成果。其中最有代表性的是Luhn在IBM公司的工作，他提出了利用词对文档构建索引并利用检索与文档中词的匹配程度进行检索 的方法，这种方法就是目前常用的倒排文档技术的雏形。

在60年代，信息检索技术的一些关键技术获取了突破。其间出现了一些优秀的系统以及评价指标。在评价指标方面，由Cranfield的研究组组织的Cranfield评测提出了许多目前仍然被广泛采用的评价指标，而在系统方面，Gernard Salton开发的SMART2系统构建了一个很好的研究平台，在此平台上，研究者可以定义自己的文档相关性测度，以改进检索性能。这样，作为一个研究课题，信息检索技术拥有了较为完善实验平台与评价指标，其研究理所当然地步入了快车道。也正因为如此，在70年代到80年代，许多信息检索的理论与模型被提出，并且被证明对当时所能获得的数据集是有效的。其中最为著名的是Gerard Salton提出的向量空间模型。至今该模型还是信息检索领域最为常用的模型之一。但是，检索的对象——文本集合的缺乏使得这些技术在海量文本上的可靠性无法得到验证。当时的研究大多针对数千篇的文档组成的集合。这时，美国国家标准技术研究所(NIST)组织的文本检索会议(Text Retrieval Conference, TREC)的召开改变了这一情况。TREC是一个评测性质的会议，为参评者提供了大规模的文本语料，从而大大推动了信息检索技术的快速发展。会议的第一次召开是1992年，不久后，互联网兴起为信息检索技术提供了一个巨大的实验场。从Yahoo到Google，大量实用的文本信息检索系统开始出现并得到广泛应用。这些系统从事实上改变了人类获取信息与知识的方式。

目前，在文本检索领域，简单的信息检索已经开始向更加复杂且人性化的垂直搜索演化，引入了信息抽取技术以提取文档中的结构化信息。

模型早期的信息检索系统采用“布尔查询”的方法来进行全文检索。这种方法无疑将构造一个合适的查询的责任推到用户身上。用户必须详细的规划自己的查询，其复杂程度不亚于编程语言。这种检索方式并不提供任何的文档相关性测度，对于文档与查询的评价就只有“匹配”，“不匹配”两种而已。这两点问题决定了布尔查询不能被广泛应用。但是，由于布尔检索能够给用户提供更多的可控制性，今天我们仍然可以在搜索引擎的“高级搜索”中找到布尔查询的身影。

对于大规模的语料库，任何检索都可能返回数量众多的结果，因此对检索结果进行排序是必须的。因此，一个好的信息检索模型必须提供文档相关性测度。一个好的测度应该使与用户查询需求最相关的那些结果，排在最前面，同时允许尽可能多的，与用户查询有一定关系的结果被包括进来。目前，最为常用的信息检索模型有三种：

向量空间模型 (Vector Space Model, VSM)

概率模型 (Probabilistic Model)

推理网络模型 (Inference Network Model)

向量空间模型向量空间模型最早由Gerard提出。在此模型中，一个文档(Document)被描述成由一系列关键词(Term)组成的向量。模型并没有规定关键词如何定义，但是一般来说，关键词可以是字，词或者短语。在语音文档检索中，还可以是混淆类、音子、音子串等等单元。假设我们用“词”作为Term，那么在词典中的每一个词，都定义向量空间中的一维。如果一篇文档包含这个词，那么表示这个文档的向量在这个词所定义的维度上应该拥有一个非0值（对绝大多数系统来说，是正值）。

当一个查询被提交时，由于这个查询也是由文本构成，所以也可以被向量空间所表示。模型将对查询与文档，计算一个相似度需要注意的是，模型也没有对相似度给出确切的定义。它可以使欧氏距离，也可以是两个向量的夹角的余弦。

假设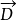 表示文档向量，而 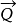表示查询向量，文档与查询的相关性可以用余弦距离表示如下：

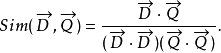
如果我们用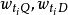 表示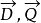 中的第 i维的值，并且对每个文档矢量进行归一化，即令 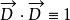，那么上式有可以表示为

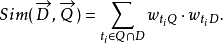
在此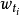，究竟如何取值是一个重要的问题，其取值一般被称为关键词i在文档D中的权重。关键词权重问题将在随后进行专门的讨论。

传统向量空间模型的一个问题是各个维度间缺乏相关性，因而无法对文档中各个词的相关性提供信息。从宏观上看，仍然没有摆脱“关键词匹配”的窠臼。一个自然的想法就是对文档特征——文档向量进行降维，将维数巨大的文档向量投影到某个较小维度的空间中，使得关键词之间即使不完全匹配，也能够根据语义发生关系。这就诞生了潜语义索引(Latent Semantic Indexing)，它通过对向量空间进行奇异值分解，将高维文档向量投射到低维潜语义空间中。潜语义索引随后被融入概率模型框架中，形成了基于概率模型的PLSI(Probabilistic Latent Semantic Indexing)， 和LDA(Latent Dirichlet Allocation)。

概率模型概率模型的基本思想是估计文档与查询相关联概率，并对所有文档根据关联概率进行排序。这一模型最早由Maron和Kuhn在1960年提出。在给定查询Q的情况下，用P(R|D)表示文档与查询相关的概率，而用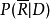表示文档与查询不相关的概率。 那么，就可以用

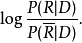对文档进行排序。利用贝叶斯公式，可以很容易的将上面的公式变为产生式的形式：

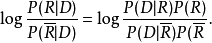由于P(R)和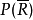同文档无关，上面的公式可以最终表示为：

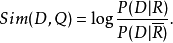概率模型的主要任务就集中在估计P(D|R)和上。

推理网络模型推理网络模型是一种较上述两中模型更为一般化的模型，上述模型都可以归结为推理网络模型的一种实现。在此模型下，仅仅规定文档以某种 “力度”产生某个来自查询的关键词，至于力度如何定义，则完全没有规定，即可以是概率，也可以是关键词权重。

倒排文档索引技术在信息检索系统的具体实现中，需要快速地找到文档中所包含的关键词。相比文档来说，关键词的个数是较少的，因此，以关键词为核心对文档进行索引是更加可行的方法。这就是信息检索领域常用的“倒排文档索引”技术。倒排文档索引可以被看成一个链表数组，每个链表的表头包含关键词，其后续单元则包括所有包括这个关键词的文档标号，以及一些其他信息。这些信息可以是文档中该词的频率，也可以是文档中该词的位置等信息。

倒排文档索引的优势不仅在于关键词个数少带来的检索效率提高，还在于其特别易于同信息检索技术结合。在实际应用中，查询中所包含的关键词往往是很少的，完全不包含查询中的所有关键词的文档，一般来说是不会被列入结果集的。因此，以关键词为主键进行索引，只需要用查询中包括的关键词，进行几次简单的查询就能够找出所有可能的文档。

倒排文档索引的具体数据结构可以进行进一步的优化。在关键词查询上，往往采用B-Tree或哈希表进行快速查询。而文档列表的数据结构则可以采用简单的无序列表进行存储，但是此种无序列表存在一个问题，就是当多个关键词对应的文档集需要进行比较的时候，比较效率将比较低。因此，在实际应用中往往采用二叉搜索树组织文档列表。

关键词权重关键词对于区分文档的作用是不同的。例如一些虚词对于区分文档的内容与查询是否相关并没有多大的意义。

对于概率模型而言，可以有完备的理论来估计每篇文档生成某个词的概率，因而其主要工作集中于如何确定较好的概率估计方法。而对于向量 空间模型来说，确定关键词权重在很大程度上依赖于研究者的经验及对文档特性的分析。

目前，对关键词权重的确定方法一般都需要获取一些关于关键词的统计量，而后根据这些统计量，应用某种认为规定的计算公式来得到权重。 最常用的统计量包括：

tf，Term Frequency的缩写，表示某个关键词在某个文档中出现的频率。

qtf，Query Term Frequency的缩写。表示查询中某关键词的出现频率。

N，集合中的文档总数

df，Document Frequency的缩写，表示文档集合中，出现某个关键词的文档个数。

idf，Inversed Document Frequency的缩写。

dl，文档长度

adl，平均文档长度

在向量空间模型下，构造关键词权重计算公式有三个基本原则：

如果一个关键词在某个文档中出现次数越多，那么这个词应该被认为越重要。

如果一个关键词在越多的文档中出现，那么这个词区分文档的作用就越低，于是其重要性也应当相应降低。

一篇文档越长，那么其出现某个关键词的次数可能越高，而每个关键词对这个文档的区分作用也越低，相应的应该对这些关键词予以一定的折扣。

早期的权重往往直接采用tf，但是显然这种权重并没有考虑上述第二条原则，因此在大规模系统中是不适用的。目前，常用的关键词权重计算公式大多基于tf和df进行构建，同时，一些较为复杂的计算公式也考虑了文档长度。现简要列举如下：

TF-IDF得分。严格地说，TF/IDF得分并不特指某个计算公式，而是一个计算公式集合。其中TF与IDF都可以进行各种变换，究竟何种变换较能匹配实际需求，需要由实验和应用来验证。

本词条内容贡献者为:

黄伦先 - 副教授 - 西南大学