[科普中国]-最小描述长度

最小描述长度( MDL) 原理是 Rissane 在研究通用编码时提出的。其基本原理是对于一组给定的实例数据 D ， 如果要对其进行保存 ，为了节省存储空间， 一般采用某种模型对其进行编码压缩，然后再保存压缩后的数据。同时， 为了以后正确恢复这些实例数据，将所用的模型也保存起来。所以需要保存的数据长度( 比特数) 等于这些实例数据进行编码压缩后的长度加上保存模型所需的数据长度，将该数据长度称为总描述长度。最小描述长度( MDL) 原理就是要求选择总描述长度最小的模型。

描述最小描述长度原则是将奥卡姆剃刀形式化后的一种结果。其想法是，在给予假说的集合的情况下，能产生最多资料压缩效果的那个假说是最好的。它是在1978年由Jorma Rissanen所引入的。在信息论和计算机学习理论中，最小描述长度原则是个重要观念。1

任一资料集都可以由一有限（譬如说，二进制制的）字母集内符号所成的字串来表示。"最小描述长度原则背后的基本想法是：在任一给定的资料集内的任何规律性都可用来压缩。亦即在描述资料时，与逐字逐句来描述资料的方式相比，能使用比所需还少的符号"（Grünwald, 1998。见底下的链接）。既然我们希望选取到的假说能抓到资料中最多的规律，于是我们则寻找压缩效果最佳的假说。

若要如此，我们首先要决定一个用来压缩资料的程式代码。最一般的方式是选一个（具有图灵完全特性的）计算机编程语言。我们接着以这个语言撰写一个会输出某笔资料的计算机程序。于是这个程式则能代表此笔资料。而能输出此资料而又最短的程式，其长度被称为此项资料的柯氏复杂性。这是Ray Solomonoff的核心概念，一个将归纳推论理想化后的理论。

然而，其想法在数学上并不提供一个实际的推论方法。最重要的理由如下：柯氏复杂度在计算理论中是不可计算的：不存在一个计算机程序，能在给予任意序列的资料情况下，输出最短而又可以产生此笔资料的程式。即使我们偶遇一个最短的程式，一般情况下也无法确知它是最短的。柯氏复杂度与使用什么电脑语言来描述程式有关。使用什么语言是可任意选择的，但一些额外的常数项会影响复杂度。基于这个理由，柯氏复杂度理论中倾向不理会常数项。但实务上，通常只有资料中的很小一部分总量是可得的，如此，则常数通常可以对于推论结果有很大的影响：好的结果不能保证能适用于有限的资料。

而最小描述长度原则则借由以下方式来试图补救上述问题：限制所能使用代码的集合。使得对于所允许的代码而言，寻找某笔资料最短的码长变成可行（可计算）的。选择一种代码，使得不论手上有什么样的资料，此代码在都是相当有效率的。这点是有些独特的（exclusive），这方面则有许多研究在进行中。比起"程式"，在最小描述长度理论的领域中，比较常用的是侯选假说、模型或代码。允许使用的代码集合则被称为模型类别。（有些作者则模型类别指为模型，这会令人混淆）于是代码描述及借助于这代码的资料描述的加总是最小的那个代码会被选取。

特征最小描述长度的一个重要特性是，它提供了一个避免过适现象的保护装置。这是因为它在假说复杂度和已知假说下的资料复杂度之间做了取舍。要理解为什么这是对的，可以考虑以下的例子。假设你抛掷一个铜板一千次，且你观察到了正反面的个数。我们考虑两种模式类别：第一种是对每个结果，以0表正面及1表反面的方式来编码。这代码所代表的假说即为这铜板是公平。根据这个编码方式所得的代码长度总是1000位元。对于一个有偏向的铜板，第二个模型类别则是，所有有效率的代码。其代表的假说即为这个铜板是不公正的。譬如，我们观察到510个正面和490个反面。于是，根据第二个模型中最佳码的所求得的码长，应少于一千位元。因为这理由，一个天真的统计方法可能提出第二个假说应是对资料较好的解释。然而，在一个最小描述长度策略中，我们必须基于假说建造一个单一码，我们不能只是用最好的那一个。一个简单的方式是，使用两部分的代码。我们先指定模型中哪一个假说拥有最佳的表现。然后指定使用这个代码的资料。我们须要不少位元去指定哪一个代码要使用。所以基于第二个模型的总码长将大于一千位元。所以，如果你服从最小描述长度策略，其结论将是，即使第二个模型类别的最佳资料可以更适应资料，仍然没有足够的证据可以支持铜板是偏向的假说。

最小描述长度核心是代码长度函数和机率分布之间的一对一且映成（牵涉到的引理为克拉夫特不等式）。 对于任意机率分布 P，去建造一代码C，其长度为C(x)等于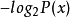是可行的；这代码最小化预期的码长。反过来说，给予一个编码C，则可以建造一个机率分布P，保持同样的结果。（在这里忽略rounding issues）。换句话说，搜寻一有效代码被化简化搜寻一个好的机率分布，反过来说亦如是。

应用如果将贝叶斯网络作为对实例数据进行压缩编码的模型， MDL原理就可以用于贝叶斯网络的学习。该度量被视为网络结构的描述长度和在给定结构下样本数据集的描述长度之和。一方面，用于描述网络结构的编码位随模型复杂度的增加而增加 ； 另一方面， 对数据集描述的编码位随模型复杂度的增加而下降。因此，贝叶斯网络的 MDL总是力求在模型精度和模型复杂度之间找到平衡。构建贝叶斯网络首先定义一个评分函数， 该评分函数描述了每个可能结构对观察到的数据拟合， 其目的就是发现评分最大的结构，这个过程连续进行到新模型的评分分数不再比老模型的高为止。

最小描述长度在分词中的应用也比较直接，就是将分词视为一种编码方式，如一个字符串，”iloveyou“ ，总共8个符号，就是对应的8个字母，经过分词后就是“i love you”，就只有3个符号，就是3个单词，这样总长度变小了，但是需要额外的信息来记录单词的信息，也就是模型。因此需要的总的长度不一定变小。

相关概念透过上述的程式码与机率分布之间的相似点，最小描述长度原理和机率论及统计学是有很密切的关连。这使得有些研究员将最小描述长度看成等同于Bayesian inference。模型的代码长度和模型及资的料代码长度则分别相当于Baysian架构中的prior probability和marginal likelihood。这观点可用David MacKay的Information Theory, Inference, and Learning Algorithms中的例子来说明。（见下面链接）然而，当用Bayesian机器建造有效率 最小描述长度 程式码有用时，最小描述长度 架构也包含其它非Bayesian的程式码。一个例子是Shtarkov的'normalized maximum likelihood code'，在目前 最小描述长度 理论中扮演一个核心角色。但不等于Bayesian推论。更进一步，Rissanen强调，对于真实资料产生过程，我们应该不做假设：实务上，一个model class在传统上是真实的减化，所以不包含任何客观角度都为真的程式码或机率分布，根据 最小描述长度 哲学，如果Bayesian方法是基于对某于可能的资料产生过会导致不好结果的不安全的priors，我们应该除去。从 最小描述长度 的观点来看，可接受的priors，通常倾向所谓的objvective Bayesian分析；然而，其动机通常是不同的。

最小描述长度并非第一个信息论来学习的策略。早在1968年，Wallace和Boulton即提倡一类似概念，称作最小讯息长度。最小描述长度和最小讯息长度的不同一直是让学界及百科编撰者困惑的来源。表面上来说，这些方法大致看似相同，但有一些主要不同，特别是在解释方法上：

最小讯息长度是一个完全面向Bayesian策略：它从这个想法开始：一假说代表其在关于资料产生过程，以prior分布表示的可信度。最小描述长度公开地避免任何关于资料产生过程的假设（但请面上面关于选择一个"合理"代码的困难）。

两种方法都使用了两部分代码：第一部分总是代表一人试图去学习的资讯，如模型类别的索引（model selection）或参数值（估计理论）第二部分则是一种资料的编码，在给予第一部分资讯的情况下。其不同是在于，在 最小描述长度 中，其建议，我们不想学到的参数应被移到第二部分的码，其中他们可以使用one-part code来和资料在一起。这通常比two-part code更有效率。在 最小讯息长度 原始描述，所有的参数是在第一部分被编码，所以会学到所有参数。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所