[科普中国]-香农熵

1948 年，香农提出了“信息熵”(shāng) 的概念，解决了对信息的量化度量问题。

一条信息的信息量大小和它的不确定性有直接的关系。比如说，我们要搞清楚一件非常非常不确定的事，或是我们一无所知的事情，就需要了解大量的信息。相反，如果我们对某件事已经有了较多的了解，我们不需要太多的信息就能把它搞清楚。所以，从这个角度，我们可以认为，信息量的度量就等于不确定性的多少。

基本定义对于任意一个随机变量 X，它的熵定义如下：

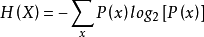
变量的不确定性越大，熵也就越大，把它搞清楚所需要的信息量也就越大。

实例我们如何来量化度量信息量呢？以世界杯赛为例。大家都很关心谁会是冠军。假如我错过了看世界杯，赛后我问一个知道比赛结果的观众“哪支球队是冠军”？ 他不愿意直接告诉我， 而要让我猜，并且我每猜一次，他要收一元钱才肯告诉我是否猜对了，那么我需要付给他多少钱才能知道谁是冠军呢? 我可以把球队编上号，从 1 到 32， 然后提问： “冠军的球队在 1-16 号中吗?” 假如他告诉我猜对了， 我会接着问： “冠军在 1-8 号中吗?” 假如他告诉我猜错了， 我自然知道冠军队在 9-16 中。 这样最多只需要五次， 我就能知道哪支球队是冠军。所以，谁是世界杯冠军这条消息的信息量只值五块钱。

此时可能会发现我们实际上可能不需要猜五次就能猜出谁是冠军，因为象巴西、德国、意大利这样的球队得冠军的可能性比日本、美国、韩国等队大的多。因此，我们第一次猜测时不需要把 32 个球队等分成两个组，而可以把少数几个最可能的球队分成一组，把其它队分成另一组。然后我们猜冠军球队是否在那几只热门队中。我们重复这样的过程，根据夺冠概率对剩下的候选球队分组，直到找到冠军队。这样，我们也许三次或四次就猜出结果。因此，当每个球队夺冠的可能性（概率）不等时，“谁世界杯冠军”的信息量的信息量比五比特少。香农指出，它的准确信息量应该是

其中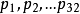，分别是这 32 个球队夺冠的概率。香农把它称为“信息熵” (Entropy)，一般用符号 H 表示，单位是比特。可以推算当 32 个球队夺冠概率相同时，对应的信息熵等于五比特。

香农熵(Shannon entropy)在生物信息领域基因表达分析中也有广泛的应用，如一些或一个基因在不同组织材料中表达情况己知，但如何确定这些基因是组织特异性表达，还是广泛表达的，那我们就来计算这些基因在N个样本中的香农熵，结果越趋近于log2(N)，则表明它是一个越广泛表达的基因，结果越趋近于0则表示它是一个特异表达的基因。1

数学分析当然，香农不是用钱，而是用 “比特”（bit）这个概念来度量信息量。 一个比特是一位二进制数，计算机中的一个字节是八个比特。在上面的例子中，这条消息的信息量是五比特。（如果有朝一日有六十四个队进入决赛阶段的比赛，那么“谁世界杯冠军”的信息量就是六比特，因为我们要多猜一次。） 读者可能已经发现, 信息量的比特数和所有可能情况的对数函数 log 有关。 ( , 。）

计算以计算一本五十万字的中文书平均有多少信息量为例。常用的汉字（一级二级国标）大约有 7000 字。假如每个字等概率，那么大约需要 13 个比特（即 13 位二进制数）表示一个汉字。但汉字的使用是不平衡的。实际上，前 10% 的汉字占文本的 95% 以上。因此，即使不考虑上下文的相关性，而只考虑每个汉字的独立的概率，那么，每个汉字的信息熵大约也只有 8-9 个比特。如果再考虑上下文相关性，每个汉字的信息熵只有5比特左右。所以，一本五十万字的中文书，信息量大约是 250 万比特。如果用一个好的算法压缩一下，整本书可以存成一个 320KB 的文件。如果我们直接用两字节的国标编码存储这本书，大约需要 1MB 大小，是压缩文件的三倍。这两个数量的差距，在信息论中称作“冗余度”（redundancy)。 需要指出的是我们这里讲的 250 万比特是个平均数，同样长度的书，所含的信息量可以差很多。如果一本书重复的内容很多，它的信息量就小，冗余度就大。

不同语言的冗余度差别很大，而汉语在所有语言中冗余度是相对小的。这和人们普遍的认识“汉语是最简洁的语言”是一致的。1

与热熵的关系熵这一名称并不是香农首先提出的。最先提出熵这一名称的是物理学家，他提出的熵现在称其为热熵，它是热力学系统的一个状态函数，热熵是物理系统无序性的量度，热熵越大，表明物理系统可能的微观状态数也就越多，从微观上看，系统就越变化多端，越没有秩序。

香农在研究随机变量不确定性量度时所得的式在数学模型层次上与热熵完全相同，所以香农也把它称作熵，现在一般称其为信息熵或香农熵。

若把系统分子的相空间作为系统宏观状态的状态空间，则按分子在相空间中的分布而求得的香农熵H与其热熵S有如下的关系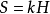： 因此，可以认为热熵是香农熵的一个特例，它仅仅是分子在相空间所处位置的不确定性的量度。

然而，热熵是有量纲的，而香农熵是无量纲的，这是两者的重大差别。2

意义对于随机变量而言，其取值是不确定的。在做随机试验之前，我们只了解各取值的概率分布，而做完随机试验后，我们就确切地知道了取值，不确定性完全消失。这样，通过随机试验我们获得了信息，且该信息的数量恰好等于随机变量的熵。在这个意义上，我们可以把熵作为信息的量度。2

本词条内容贡献者为:

鄢志丹 - 副教授 - 中国石油大学（华东）