[科普中国]-非限覆盖曲面

覆盖曲面是黎曼曲面理论中引进的重要概念。非限覆盖曲面是常见的三种覆盖曲面之一。

简介σ 为投影映射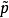，是 p 上的点， p 为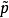的投影。设和 r 分别是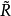和 R 上的曲线，若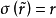，则称是 r 的提升。若对任意的 R 上的曲线 r 和 r 的起始点上的任意点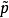，r 的以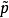为起始点的提升总存在，则称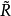为 R 的非限覆盖曲面。

性质单值性定理称：若是 R 的非限覆盖曲面，r1 和 r2 为 R 上任两个同伦曲线，它们的以共同起始点 p0上的一点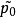为起始点的提升分别为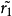和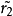，则它们亦有相同的终点，且是同伦的。

投影映射作为连续映射诱导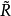的基本群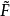与 R 的基本群 F 的子群 G 同构，并称 G 为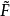的迹群，记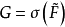。反之，对 R 的基本群 F 的任意子群 G ，恒存在一个非限覆盖曲面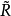，使得其基本群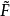的迹群为 G 。1

黎曼曲面在数学中，黎曼曲面是德国数学家黎曼为了给多值解析函数设想一个单值的定义域而提出的一种曲面。用现代的语言说，黎曼曲面就是连通的一维复流形。

黎曼曲面的研究不仅是单复变函数论的基本问题之一，而且与众多的现代数学分支有紧密联系，如多复变函数论、复流形、代数几何、代数数论、 自守函数等。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学