区间消去法(interval elimination method)是求单变量函数无约束极值的较实用的一类直接搜索方法,其特点是在搜索过程中,不断缩小最优点所在的区间,即通过搜索区间的逐步缩小来确定最优点1。
基本介绍当已确定了初始单谷区间之后,就可以进行一维寻优。实用的一维寻优方法一般可以分为区间消去法和函数逼近法两种。
所谓区间消去法(又称试探法),就是不断消去不存在最优点的区间,使搜索区间越来越短.最终寻得近似最优点。为了在每次迭代中缩短区间,需要在区间内插入计算点并求出其函数值。插入点的位置则因方法的不同而异,一般是按某种给定的规则来确定区间内插入点的位置,此点位置的确定仅仅按照区间缩短如何加快,而不顾及函数值的分布关系。属于这种方法的有裴波纳契(Fibonacci)法、黄金分割法(0.618法)等。
函数逼近法(又称插值法或近似法),是用一个多项式来近似代替目标函数,并用这个多项式的极小点作为目标函数的近似最优点。这个多项式是根据某些点处的某些信息,如函数值、一阶导数、二阶导数等构造出来的。属于这种方法的有牛顿法(切线法)、二次插值法(抛物线法)等2。
区间消去法原理搜索区间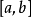 确定之后,采用区间消去法逐步缩短搜索区间,从而找到极小点的数值近似解。假定在搜索区间
确定之后,采用区间消去法逐步缩短搜索区间,从而找到极小点的数值近似解。假定在搜索区间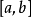 内任取两点
内任取两点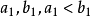 ,并计算函数值
,并计算函数值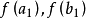 。于是将有下列三种可能情形2:
。于是将有下列三种可能情形2:
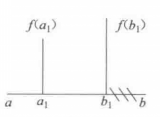
(1)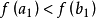 ,如图1(a)所示。由于函数值为单谷,所以极小点必在区间
,如图1(a)所示。由于函数值为单谷,所以极小点必在区间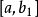 内。
内。
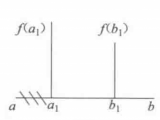
(2)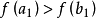 ,如图1(b)所示。同理,极小点应在区间
,如图1(b)所示。同理,极小点应在区间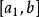 内。
内。
(3)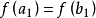 ,如图1(c)所示。这时极小点应在区间
,如图1(c)所示。这时极小点应在区间 内。
内。
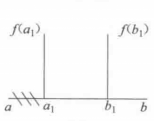
根据以上所述,只要在区间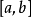 内取两个点,算出它们的函数值并加以比较,就可以把搜索区间
内取两个点,算出它们的函数值并加以比较,就可以把搜索区间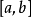 缩短成
缩短成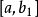 ,
,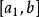 或
或 。应当指出,对于第一种情况,我们已算出区间[
。应当指出,对于第一种情况,我们已算出区间[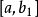 内
内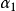 点的函数值,如果把搜索区间
点的函数值,如果把搜索区间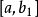 进一步缩短,只需在其内再取一点算出函数值并与
进一步缩短,只需在其内再取一点算出函数值并与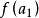 加以比较,即可达到目的。对于第二种情况,同样只需再计算一点的函数值就可以把搜索区间继续缩短。第三种情形与前面两种情形不同,因为在区间
加以比较,即可达到目的。对于第二种情况,同样只需再计算一点的函数值就可以把搜索区间继续缩短。第三种情形与前面两种情形不同,因为在区间 内缺少已算出的函数值。要想把区间
内缺少已算出的函数值。要想把区间 进一步缩短,需在其内部取两个点(而不是一个点)计算出相应的函数值再加以比较才行。如果经常发生这种情形,为了缩短搜索区间,需要多计算一倍数量的函数值,这就增加了计算工作量。因此,为了避免多计算函数值,我们把第三种情形合并到前面两种情形中去。例如,可以把前面三种情形改为下列两种情形:
进一步缩短,需在其内部取两个点(而不是一个点)计算出相应的函数值再加以比较才行。如果经常发生这种情形,为了缩短搜索区间,需要多计算一倍数量的函数值,这就增加了计算工作量。因此,为了避免多计算函数值,我们把第三种情形合并到前面两种情形中去。例如,可以把前面三种情形改为下列两种情形:
(1)若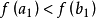 ,则取
,则取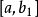 为缩短后的搜索区间。
为缩短后的搜索区间。
(2)若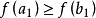 ,则取
,则取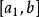 为缩短后的搜索区间。
为缩短后的搜索区间。
在实际计算中,最常用的区间消去法是裴波纳契法和黄金分割法(0.618法)2。
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国