[科普中国]-泰特猜想

泰特猜想(Tait's conjecture)是关于图的着色的一个著名猜想，3正则图的3边正常着色称为泰特着色。泰特猜想：每个简单3正则3连通平面图都有泰特着色，它与四色猜想等价，泰特(P.G.Tait)曾根据“每个3正则3连通平面图都是哈密顿图”的错误假设，给出了四色猜想的一个“证明”，塔特(W.T.Tutte)于1946年构造了一个3正则3连通的平面图，在这图上不存在哈密顿图，这个图称为塔特图，由此推翻了泰特于1880年给出的四色猜想的“证明”1。

基本介绍对于复阿贝尔簇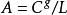 ，它的子群 同构于加法群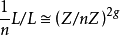 ．如果A是定义在数域K上，将 中所有点的坐标添加到K中，形成K的一个扩域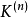 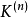， 是K的代数闭包量 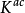的子域。伽罗瓦群 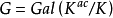作用在子群A[n]上，给出G在 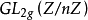上的伽罗瓦表示，现在取素数 ，则有自然满同态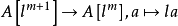 ，于是有极限 ，这叫作阿贝尔簇A的泰特模。由极限过程知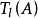， 群同构于 ，其中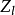 是1-adic整数环。群G通过取极限作用在 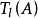上，从而给出G在 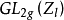中的1-adic表示。进而，若B是定义在K上的另一个阿贝尔簇，则所有从A到B的群同态形成加法群 ，而与G作用可交换的从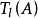 到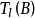 的群同态形成群 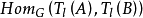，泰特猜想是说：

(1)G到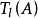 上的1-adic表示 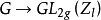是半单的；

(2)有群同构 ．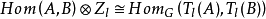

每个同态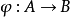 自然诱导出泰特模之间的一个同态 ，而猜想(2)本质上相当于说： 由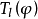 所决定，即阿贝尔簇之间的同态由它在泰特模上的作用所决定，并且 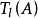到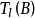 的每个G-同态都是由某个 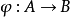诱导出来的2。

泰特猜想的证明法尔廷斯首先证明了泰特猜想，然后由泰特猜想再推出关于阿贝尔簇的沙法列维奇猜想，这也就证明了关于曲线的沙法列维奇猜想和莫代尔猜想。

法尔廷斯证明泰特猜想和关于阿贝尔簇的沙法列维奇猜想的方法本质上是费马于三百年前发明的无穷下降法，费马在证明方程 没有正整数解时，他假定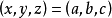 是一组正整数解，由此又导出另一组正整数解 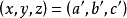，使得c'