[科普中国]-投资问题

投资问题(investment problem)是一种特殊的0-1整数规划问题。投资问题就是考虑如何将有限的资金投入到若干个项目中，以获得最大的投资回报，当问题中仅有一个不等式约束条件时，它就是背包问题1。

数学模型投资问题是一种特殊的0-1整数规划问题，数学模型为

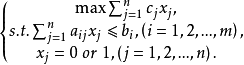它可以解释为有n个投资项目可供选择，这里的cj表示从第j项投资可得到的收益，aij表示第i种资源用于第j项投资的数量，bi表示第i种资源的限量，目标是在各种资源不超过限量bi的条件下，对哪些项目投资，才使整个投资的总效益为最大?当问题中仅有一个不等式约束条件时，它就是背包问题1。

例题解析【例1】 某公司现有资金3 000万元，今后五年内计划对以下项目进行投资2。

项日A：从第一年到第五年每年年初都可以投资，当年年末能收回本利105%。

项目B：从第一年到第四年每年年初都可以投资，次年年末收回本利135%，但规定每年最大投资额不能超过450万元。

项目C：第三年年初可以投资，到第五年年末能收回本利130%，但规定最大投资额不能超过l 200万元。

项目D：第二年年初可以投资，到第五年年末能收回本利140%，但规定最大投资额不能超过1 500万元。

试决策这些项目每年的投资额，从而使第五年末拥有自己的本利金额最大2。

分析：设梳为第；年初投资于项目/的金额（万元）。

第一年：该公司年初有资金3 000万元，因此：。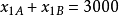

第二年：该公司在第二年初拥有资金仅为项目A在第一年投资额所收回的本息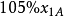，因此。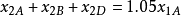

第三年：第三年年初的资金额是从项目A第二年投资和项目B第一年投资所回收的本息总和，即

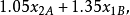故有

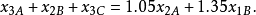
同理，第四年可得：

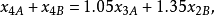
第五年为

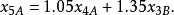
因此，线性规划模型为

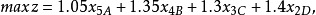
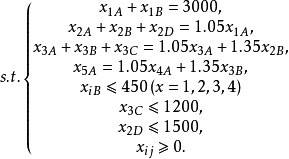
本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所