[科普中国]-模糊偏序关系

模糊偏序关系(fuzzy partially ordered relations)是论域X上的一个模糊关系，它满足自反性、可传递性以及完全反对称性，即当x≠y， R(x，y)>0时，必有R(y，x)=0。1

基本介绍设 ，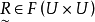

(1)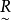 叫做具有模糊自反性，或者说 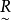是模糊自反关系，是指，每个 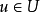，都能使 。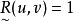

(2)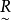 叫做具有模糊完全反对称性，或者说 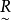是模糊完全反对称关系，是指，由 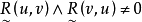必可推出u=v。

(3)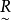 叫做具有模糊传递性，或者说 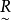是模糊传递关系，是指对任何 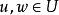，不等式

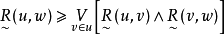永远成立。其中“ 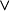”表示上确界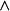，“ ”表示下确界。

关于U上的模糊关系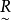 具有模糊完全反对称性的逆否命题是：对任何 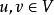由u≠v，必可推出 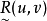和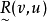 中至少有一个必为零。我们知道，逆否命题与原命题是等价的，为了使用方便，这里用它的逆否命题。

(1)具有模糊自反性及模糊传递性的模糊关系叫做模糊预序关系。

(2)具有模糊自反性、模糊完全反对称性及模糊传递性的模糊关系叫模糊偏序关系。

在论域U上给定模糊偏序关系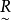 ，又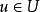 ，当且仅当U的其他元素v≠u都使 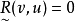时，u叫做对 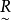来说的优越元。

有数学理论保证，在有限论域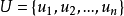 中，借助模糊偏序关系 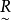必然可以排出U中元素的优越次序2。

相关介绍排序方法利用模糊偏序关系矩阵排序的具体步骤如下：

第一步，借助有限论域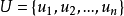上的n阶模糊偏序关系方阵R得到U的第一优越元，即在方阵R中第i列，除了主对角线上的元素是1以外，其余的元素都是零，那么ui就是第一优越元。其中。

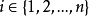第二步，划去第一优越元所在的行和列，得到新的n-1阶模糊偏序方阵，用同样的方法得到优越元作为整体的第二优越元。

如此类推，可将U中所有元素排出一定的优越次序2。

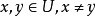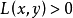模糊偏序和模糊线性序定义 称模糊偏序L为U到U的模糊线性序，如果对任意，则或。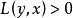

下面给出的定理说明了模糊偏序和模糊线性序的关系3。

设P是U上的模糊偏序，则必存在V(V与U有相同的有限基数)上的模糊线性序和U到V的一一映射σ，使得：若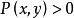，则

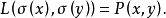
本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所