[科普中国]-模糊集表现定理

模糊集表现定理(representation theorem of fuzzy sets)是模糊集合论中的一个基本定理，表现定理的意义是：X上任给一个集合套都可以拼成一个模糊集，表现定理在理论上解释了模糊集与区间集的关系，说明模糊的对象可以由一系列赋予某种可能性度量的精确对象表述。

基本介绍模糊集表现定理与模糊集的分解定理从不同的角度揭示了模糊集与经典集的关系，分解定理表明，任一模糊集A可由集合套 来表示；而表现定理指出，每个集合套都可以表示一个模糊集1。

集合套的交并补设映射 满足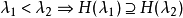： ，则称H为X上的一个集合套，所有X上的集合套组成的集合记为H(X)，在H(X)中定义运算∪，∩，如下：

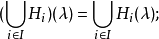
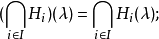
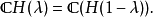
模糊集的表现定理模糊集的表现定理为：设F(X)为X上所有模糊集组成的集合，令

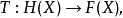
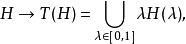则T是 到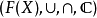 上的同态满射，且满足：

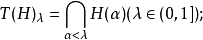
其中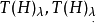分别表示模糊集T(H)的λ水平集和弱λ水平集1。

关于表现定理的代数说明表现定理阐明了一个重要事实：模糊集可由一族互相嵌套的经典集合构造出来．这就预示着模糊集合会保留经典集合的一些性质。事实上，模糊集合的运算确实保持了经典集合的大部分性质，只有互补律不成立，当我们在集合套上也定义其并、交、补运算时，可用代数学中的同态、同构来更清楚地说明相关关系。如上所述集合套的并、交、补。

集合套的并、交运算就是用经典集合的并、交来定义的，因此模糊集保持关于并、交运算的性质就是自然的事了。同时，也因为集合套的补运算涉及了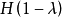，因而涉及补运算的互补律在集合套运算中不再保持，从而在与其同构的模糊集运算中也就不成立2。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所