[科普中国]-牛顿二项式

在初等代数中，二项式定理（英语：Binomial theorem）描述了二项式的幂的代数展开。根据该定理，可以将两个数之和的整数次幂诸如(x + y)n 展开为类似 axbyc 项之和的恒等式，其中b、c均为非负整数且b + c = n。系数a是依赖于 和b的正整数。当某项的指数为0时，通常略去不写。

历史杨辉三角形 主条目：杨辉三角形

二项式系数的三角形排列通常被认为是法国数学家布莱兹·帕斯卡的贡献，他在17世纪描述了这一现象。但早在他之前，就曾有数学家进行类似的研究。例如，古希腊数学家欧几里得于公元前4世纪提到了指数为2的情况。公元前三世纪，印度数学家青目探讨了更高阶的情况。帕斯卡三角形的雏形于10世纪由印度数学家大力罗摩发现。在同一时期，波斯数学家卡拉吉（英语：Al-Karaji）和数学家兼诗人欧玛尔·海亚姆得到了更为普遍的二项式定理的形式。13世纪，中国数学家杨辉也得到了类似的结果。卡拉吉（英语：Al-Karaji）用数学归纳法的原始形式给出了二项式定理和帕斯卡三角形(巴斯卡三角形)的有关证明。艾萨克·牛顿勋爵将二项式定理的系数推广到有理数。

定理的陈述根据此定理，可以将x+y的任意次幂展开成和的形式

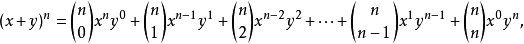
其中每个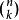 为一个称作二项式系数的特定正整数，其等于 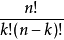。这个公式也称二项式公式或二项恒等式。使用求和符号，可以把它写作

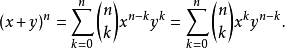
后面的表达式只是将根据x与y的对称性得出的，通过比较发现公式中的二项式系数也是对称的。 二项式定理的一个变形是用 1 来代换y得到的，所以它只涉及一个变量。在这种形式中，公式写作

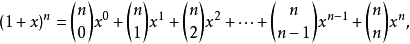或者等价地

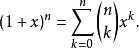
应用[编辑]牛顿以二项式定理作为基石发明出了微积分。其在初等数学中应用主要在于一些粗略的分析和估计以及证明恒等式等。

证明组合恒等式二项式定理给出的系数可以视为组合数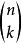 的另一种定义。 因此二项式展开与组合数的关系十分密切。 它常常用来证明一些组合恒等式。比如证明

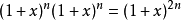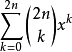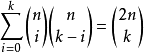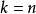可以考虑恒等式。 展开等式左边得到： 。 注意这一步使用了有限求和与乘积可以交换的性质。 同时如果展开等式右边可以得到 。 比较两边幂次为k的项的系数可以得到: 。 令 ，并注意到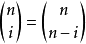 即可得到所要证明的结论。

多倍角恒等式在复数中，二项式定理可以与棣莫弗公式结合，成为多倍角公式。根据棣莫弗公式：

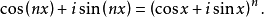
通过使用二项式定理，右边的表达式可以扩展为

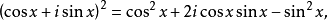
由棣莫弗公式，实部与虚部对应，能够得出

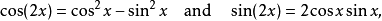
即二倍角公式。同样，因为

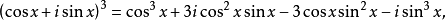
所以藉棣莫弗公式，能够得出

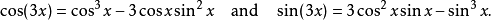
整体而言，多倍角恒等式可以写作

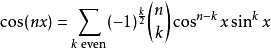
和

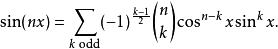
e级数e数学常数e的定义为下列极限值：

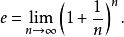
使用二项式定理能得出

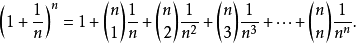
第k项之总和为

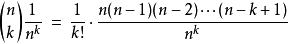
因为n→∞，右边的表达式趋近1。因此

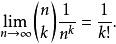
这表明e可以表示为

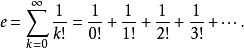
推广该定理可以推广到对任意实数次幂的展开，即所谓的牛顿广义二项式定理：

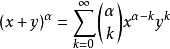。其中。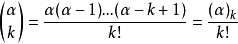

多项式展开主条目：多项式定理

对于多元形式的多项式展开，可以看做二项式定理的推广1：
.

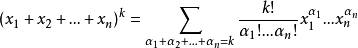证明：

数学归纳法。对元数n做归纳：
当n=2时，原式为二项式定理，成立。
假设对n-1元成立，则：

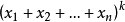
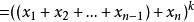
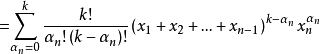
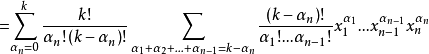
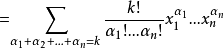
证毕

本词条内容贡献者为:

刘燕兵 - 副研究员 - 中国科学院信息工程研究所