[科普中国]-降采样

在数位信号处理领域中，降采样，又作减采集,是一种多速率数字信号处理的技术或是降低信号采样率的过程，通常用于降低数据传输速率或者数据大小。 跟插值互补，插值是用来增加取样频率。降采样的过程中会运用滤波器降低混叠造成的失真，因为降采样会有混叠的情形发生，系统中具有降采样功能的部分称为降频器。

简介降采样因子（常用表示符号为"M"）一般是大于1的整数或有理数。这个因子表达采样周期变成原来的M倍，或者等价表示采样率变成原来的1/M倍。 采样率的降低会造成频谱的压缩，因此需要利用滤波器确保在较低的采样频率下不发生混叠，确保奈奎式采样定理依旧成立。

整数倍降采样降采样整数M倍的过程可以被分解成两个部分：

利用数位低通滤波器去除讯号中的高频成分防止混叠。

对过滤高频后的讯号降采样M倍，换言之，保留原讯号中间隔为M的取样点

若仅少了第一个步骤，讯号的高频成分会在降低采样速率的过程中被混入低频讯号中，这样的失真效应我们称为混叠，因此第一个步骤是为了降低混叠影响至可以接受的程度，降采样中的滤波器称为反混叠滤波器，下面讨论如何设计反混叠滤波器。

若用无限脉冲响应的方法设计反混叠滤波器，则滤波的过程需要在降低采样速率前从输出端回传资讯到输入端，若用有限脉冲响应的方法设计反混叠滤波器，滤波的过程较为简单因为我们只需要考虑间隔为M的采样点，滤波的过程表示成：

序列h[·]是数位滤波器的脉冲响应、K是它的长度，序列x[·]为要被降采样的原始讯号的取样点，一般来说在算出y[n]后计算y[n+1]最简单的方法是让x[·]的索引增加M然后重新计算卷积，在大部分的情况下M=2，h[·]可以被设计成半频带滤波器，序列h[k]中将近一半的系数为0，因此卷积的计算过程会被大大简化。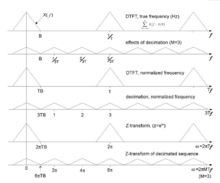

每隔M个取样点取样脉冲响应的系数成为一个次序列，总共有M个降采样的脉冲响应次序列，内积的结果是每个次序列．跟对应的取样点x[·] 内积的总和。 此外,由于采样周期变成M倍，每个降采样后的次序列会独立在每个内积中，数列x[·] 的采样点只会出一组内积之中而不会出在其他组的内积里，因此可以用M组有限长度频率响应数位滤波器同时多工地算出M组内积，M组输出值最后平行加总。这个观点提供不同的硬件实作方法，很可能适合多处理器的架构。 换句话说，输入的串流经过分工并送去M组滤波器并将输出加总，上述的架构称为多项位滤波器。1

图一: 3种不同的常见频率单位下的降采样频谱效应比较。

反混叠滤波器

我们可以从图一的三组波型中了解为何降采样的过程需要反混叠滤波器，注意三组波型图除了横轴的单位不同以外其余皆相同。 每一组波形图的第一张图是取样讯号x(t)，经过傅立叶转换得到的周期性频谱，X(f)；第二章图为取样讯号x(t)以1/3倍采样速率降取样后经过傅立叶转换得到的周期性频谱。 对于这三组波型，混叠不发生的条件同为：T为采样的时间间格，1/T为采样速率，1/2T为奈奎氏取样频率，反混叠滤波器借由设计截止频率小于1/M倍的奈奎氏取样频率确保混叠不会发生。

最上面那组图片的上面那张图的横轴代表离散时间傅立叶转换，也就是X(f)的傅立叶级数表示方式：

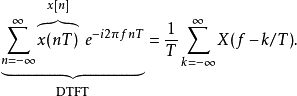
T的单位为秒，f的单位为赫兹。将MT取代公式中的T我们可以得到以1/M倍速率采样后的数列的离散时间傅立叶转换，x[nM]:

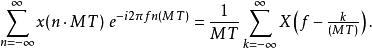
这个周期性的讯号以较低速率采样过后，频率跟振幅都被降低了1/M倍，如同图一的第二张图所示，当X(f)与附近的波型重叠，混叠将会发生，反混叠滤波器的目的就是在于确保降采样后周期降低但不会发生波型重叠，也就是混叠。

中间那组图频率f的单位改为标准化频率，这时周期为1而0.5的位置对应到奈奎氏取样频率，一般反混叠滤波器的设计会以图形的频率单位为标准，因此截止频率也要改由以标准化频率作为单位，此时截止频率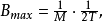被标准化为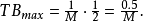这个值的单位为（秒/取样）*（周期数/秒）=周期数/取样。

最下面那组图形为原本数列以及以低速率取样后数列的Z转换，受到复数变数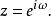的限制，x[n]的数列的形式为傅立叶级数，与1比较，我们推论：

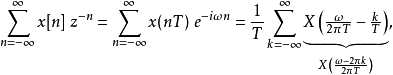
这个方程式描述了图一中第五张图，同理，第六章图为：

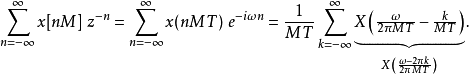
分数倍降采样令 M/L代表降采样因子，M,L都是整数，M>L，分数倍降采样可以被分解成两个步骤

以L倍频率升采样

以1/M倍频率降采样

升采样需要低通滤波器过滤资料数率增加的讯号，降采样需要低通滤波器过滤输入讯号，因此这两个滤波过程可以被和而为一，借由用单一个低通滤波器取代，此单一低通滤波器的截止频率为两者低通滤波器的低者。当M > L, 反混叠滤波器的截止频率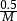（周期数/取样）会是较低的截止频率。。

bit/样本) × 2 (声道)）降低至705,600位元秒。

本词条内容贡献者为:

曹慧慧 - 副教授 - 中国矿业大学