拉格朗日括号法国数学家和力学家 J.-L.拉格朗日研究正则变换时所用的一种数学符号。拉格朗日括号是一种与泊松括号关系密切的运算,1808年至1810年间由约瑟夫·拉格朗日最早用于经典力学之中。不过与泊松括号相比,拉格朗日括号已不常使用。
定义令(q1, …,qn,p1, …,pn)为相空间中的正则坐标,且每一个坐标都可表示为两个变量u与v的函数,则u和v的拉格朗日括号为:

性质拉格朗日括号与特定的正则坐标无关(q,p)。如取另一组正则坐标(Q,P)=(Q1, …,Qn,P1, …,Pn),满足正则变换
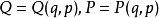
此时拉格朗日括号不变,即
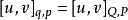
因而通常情况下会省略下标。
如果2n维相空间W上有辛形式Ω,u1,…,u2n是W上的一个坐标系,那幺正则坐标(q,p)可表示为u的函数,而拉格朗日括号所组成的矩阵
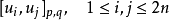
表示Ω在坐标系u下的分量,可看作一个张量。这个矩阵是由泊松括号所组成的矩阵
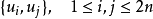
的逆矩阵。1
由上述性质可以得到,相空间上的坐标(Q1, …,Qn,P1, …,Pn)是正则的,当且仅当它们之间的拉格朗日括号有如下形式:
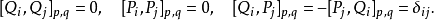
本词条内容贡献者为:
李宗秀 - 副教授 - 黑龙江财经学院




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国