[科普中国]-逻辑斯谛方程

逻辑斯蒂方程( Logistic Equation) 是数学生物学家 Pierre - Francois Verhulst 提出的著名的人口增长模型，为马尔萨斯( Malthus) 人口模型的推广，从其问世以来，它的应用从人口增长模型拓展到很多领域，广泛应用于生物学、医学、经济管理学等方面。

方程描述逻辑斯谛（Logistic）方程,即常微分方程: .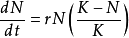

该模型建立在人口增长率 dy 和人口数量 y( t) 成正比，dt

并且处于理想状态( 如没有天敌、免于疾病等) 下，而且只考虑出生率和死亡率，没有考虑环境因素。事实上，更有实际意义的模型应该能反映限定环境的情况，这是由于很多种群开始时是呈指数增长的，但数量接近 K( K 为环境容纳量，也称为承载能力) 时增长率逐渐下降。显然方程( 2) 只能反映第一种趋势，而方程( 1) 则考虑了上述两个趋势，因此逻辑斯蒂方程的应用就更加广泛。一般而言，如果客观事物的数量特征是: 在时间 t 很小时，事物呈指数型增长，而当 t 增大时，增长速度逐渐下降，且越来越接近于一个确定的值( 即承载能力 K) ，此类问题可用逻辑斯蒂方程加以解决.1

方程应用逻辑斯蒂方程建立时是 Verhulst 提出的人口增长模型，因此该方程在人口增长和预测方面应用较多，但在其它方面的应用也非常广泛。1

销售预测：通常某种新产品开始销售时，由于消费者对它的产品特点及功能了解不多，销售量也就很小，但伴随着该产品的大量信息通过媒体等相关渠道传播出去后，其销售量逐渐增加，在市场快接近饱和时销售量的增长速度又变得比较缓慢。这一数量特征和逻辑斯蒂方程所描述的数量特征相吻合。因此在销量增加的过程中，每一时间段该产品生产数量的多少可根据逻辑斯蒂方程进行预测，便于厂家结合预测数据组织生产。2

城市洪水事件研究逻辑斯蒂回归分析就是用来解决因变量是分类变量的一种统计分析方法，它能在最大程度上客观地反映致灾因子与灾害发生之间的关系.但是逻辑斯蒂回归模型在国内应用并不多见，仅有少数将该模型引入滑坡、泥石流灾害的评估中,取得很好的效果.该模型在洪水研究方面的应用几乎很少见，因此本研究尝试利用GIS的空间分析功能,采用逻辑斯蒂回归方法对兰州洪水事件进行验证,效果良好。

意义当一个物种迁入到一个新生态系统中后,其数量会发生变化.假设该物种的起始数量小于环境的最大容纳量,则数量会增长.增长方式有以下两种:

1 J型增长 若该物种在此生态系统中无天敌,且食物 空间等资源充足(理想环境),则增长函数为N(t)=n(p^t).其中,N(t)为第t年的种群数量,t为时间,p为每年的增长率(大于1).图象形似J形.

2 S型增长 若该物种在此生态系统中有天敌,食物 空间等资源也不充足(非理想环境),则增长函数满足逻辑斯谛方程.图象形似S形.此方程是描述在资源有限的条件下种群增长规律的一个最佳数学模型。

本词条内容贡献者为:

赵阳国 - 副教授 - 中国海洋大学