[科普中国]-约束优化问题

约束优化问题（亦译为受约束的最优化问题）是一类数学最优化问题，它由目标函数以及与目标函数中的变量相关的约束条件两部分组成，优化过程则为在约束条件下最优化（最大化或最小化）目标函数。

方程一般形式一个约束最小化问题可以写成如下形式:

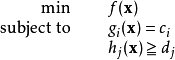其中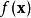 是目标函数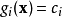； 与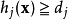 是求解这个目标函数需要满足约束条件（i和j标识第几个约束条）。在这个例子中，所有约束条件都是必须满足的，为硬约束。在有些问题中，目标函数是一些成本函数或者效用函数的加总，个体成本函数或者效用函数的约束条件只需要尽量满足，而不是必须满足，这种情况下的约束条件为软约束。1

约束 (数学)在数学中，约束是一个最佳化问题的解需要符合的条件。约束可分为等式约束及不等式约束。符合所有约束的解的集合称为可行集（feasible set）或是候选解（candidate solution）。1

效用效用（英语：Utility），是微观经济学中最常用的概念之一。一般而言，效用是指对于消费者通过消费或者享受闲暇等使自己的需求、欲望等得到的满足的一个度量。

历史效用的概念是丹尼尔·伯努利在解释圣彼得堡悖论（丹尼尔的表兄尼古拉一世·伯努利设计出来的一个悖论）时提出的，目的是挑战以金额期望值(expected monetary value, EMV)作为决策的标准。

丹尼尔·伯努利对这个悖论的解答在1738年的论文里，主要包括两条原理：

边际效用递减原理：一个人对于财富的占有多多益善，即效用函数一阶导数大于零；随着财富的增加，满足程度的增加速度不断下降，效用函数二阶导数小于零。

最大效用原理：在风险和不确定条件下，个人的决策行为准则是为了获得最大期望效用值而非最大期望金额值。

效用的基数性和序数性经济学家对于效用的理解是有一个过程的。19世纪的杰文斯、瓦尔拉斯和马歇尔等早期经济学家认为效用如同人们的身高和体重一样是可以测量的，而希克斯（John Hicks，1946）则尝试了只在序数性效用的假定下，也取得了很多的研究成果。希克斯认为，效用的数值表现只是为了表达偏好的顺序，并非效用的绝对数值。从教科书等内容判断，现在比较通用的应该是后者的序数性效用。1

相关条目卡罗需－库恩－塔克条件

拉格朗日乘数

水平集

线性规划

非线性规划

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学