[科普中国]-多主体优化系统

多主体优化系统 (multiagent optimization system, MAOS) 是一种基于混合多主体系统和群集智能的优化系统。它已经被用来求解数值优化和组合优化问题，如旅行商问题、图着色问题、背包问题等。

组合优化组合最优化，在应用数学和理论计算机科学的领域中，组合优化是在一个有限的对象集中找出最优对象的一类课题。在很多组合优化的问题中，穷举搜索/枚举法是不可行的。组合优化的问题的特征是可行解的集是离散或者可以简化到离散的，并且目标是找到最优解。常见的例子有旅行商问题和最小生成树。二维的例子，比如服装厂做衣服，衣服分成很多块，这些块需要从布料上切下来。怎么切，剩下的废布料最少？三维的例子，如集装优化。

组合优化的难处，主要是加进来拓扑分析，不同的拓扑形态下，不同部分的约束关系便不同，算法也就要调整。如果给定一个拓扑形态，组合优化往往就退化成一个整数优化的问题了。1

群集智能群集智能(Swarm intelligence, SI)是一种研究分散型的自组织系统中的集体行为的人工智能技术。

典型的群集智能系统由一群简单的主体构成，每个主体和其它主体以及它们的环境作局部的交互。尽管通常没有集中控制机制来指示这些主体如何协作，但这些简单的局部交互行为通常能涌现出复杂的全局行为。当前主要的几种群集智能方法包括蚁群算法和粒子群优化。1

背包问题背包问题（Knapsack problem）是一种组合优化的NP完全问题。问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。

相似问题经常出现在商业、组合数学，计算复杂性理论、密码学和应用数学等领域中。也可以将背包问题描述为决定性问题，即在总重量不超过W的前提下，总价值是否能达到V。1

图着色问题图着色问题（英语：Graph Coloring Problem，简称GCP），又称着色问题，是最著名的NP-完全问题之一。

给定一个无向图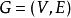，其中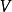为顶点集合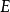，为边集合，图着色问题即为将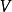分为K个颜色组，每个组形成一个独立集，即其中没有相邻的顶点。其优化版本是希望获得最小的K值。1

旅行推销员问题旅行推销员问题（最短路径问题）（英语：Travelling salesman problem,TSP）是这样一个问题：给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。它是组合优化中的一个NP困难问题，在运筹学和理论计算机科学中非常重要。

TSP是旅行购买者问题与车辆路径问题的一种特殊情况。

在计算复杂性理论中，TSP的做决定版本（其中，给定长度L，任务是决定图中是否有路径比L还要短）属于NP完全问题。因此随着城市数量的增多，任何TSP算法最坏情况下的运行时间都有可能随着城市数量的增多超多项式（可能是指数）级别增长。

问题在1930年首次被形式化，并且是在最优化中研究最深入的问题之一。许多优化方法都用它作为一个基准。尽管问题在计算上很困难，但已经有了大量的启发式和精确方法，因此可以完全求解城市数量上万的实例，并且甚至能在误差1%范围内估计上百万个城市的问题。

甚至纯粹形式的TSP都有若干应用，如企划、物流、芯片制造。稍作修改，就是DNA测序等许多领域的一个子问题。在这些应用中，“城市”的概念用来表示客户、焊接点或DNA片段，而“距离”的概念表示旅行时间或成本或DNA片段之间的相似性度量。TSP还用在天文学中，观察很多源的天文学家希望减少在源之间转动望远镜的时间。许多应用（如资源或时间窗口有限）中，可能会加入额外的约束。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学