[科普中国]-凸优化

凸优化，或叫做凸最优化，凸最小化，是数学最优化的一个子领域，研究定义于凸集中的凸函数最小化的问题。

简介凸优化，或叫做凸最优化，凸最小化，是数学最优化的一个子领域，研究定义于凸集中的凸函数最小化的问题。凸优化在某种意义上说较一般情形的数学最优化问题要简单，譬如在凸优化中局部最优值必定是全局最优值。凸函数的凸性使得凸分析中的有力工具在最优化问题中得以应用，如次导数等。

凸优化应用于很多学科领域，诸如自动控制系统，信号处理，通讯和网络，电子电路设计，数据分析和建模，统计学（最优化设计），以及金融。在近来运算能力提高和最优化理论发展的背景下，一般的凸优化已经接近简单的线性规划一样直捷易行。许多最优化问题都可以转化成凸优化（凸最小化）问题，例如求凹函数f最大值的问题就等同于求凸函数 -f最小值的问题。1

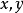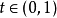凸函数凸函数是一个定义在某个向量空间的凸子集C（区间）上的实值函数f，如果在其定义域C上的任意两点，以及，有

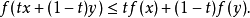也就是说，一个函数是凸的当且仅当其上境图（在函数图像上方的点集）为一个凸集。

如果对于任意的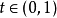有

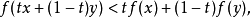函数f是严格凸的。

若对于任意的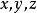，其中，都有

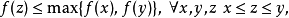则称函数f是几乎凸的。1

举例以下问题都是凸优化问题，或可以通过改变变量而转化为凸优化问题：

最小二乘

线性规划

线性约束的二次规划1

半正定规划

方法凸优化（凸最小化）问题可以用以下几种方法求解：

捆集法

次梯度法1

内点法

凸最大化通常凸优化的定义要求目标函数f在可行域内被最小化，而在某些的线性规划问题中也会研究最大化。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学