[科普中国]-勒夫纳微分方程

勒夫纳微分方程是一类偏微分方程。若f(z,t)是勒夫纳微分方程在初始条件f(z,0)=z下的解，则它的像域是由单位圆盘除去从单位圆周上的一点出发而不通过原点的一条若尔当弧后所得到的域。

简介勒夫纳微分方程是一类偏微分方程。

所谓勒夫纳微分方程是指方程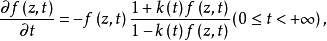 这里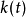是模等于1的连续复值函数。1

意义若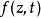是勒夫纳微分方程在初始条件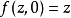下的解，则它的像域是由单位圆盘除去从单位圆周上的一点出发而不通过原点的一条若尔当弧后所得到的域。

任何满足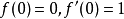的在单位圆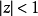内单叶解析的函数都可以用形如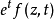的函数任意精确地逼近。

偏微分方程偏微分方程是包含未知函数的偏导数（或偏微分）的方程。

方程中所出现未知函数偏导数的最高阶数，称为该方程的阶。

在数学、物理及工程技术中应用最广泛的，是二阶偏微分方程，习惯上把这些方程称为数学物理方程。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学