[科普中国]-范·德·瓦尔登猜想

范·德·瓦尔登猜想(Van der Waerden conjecture)是关于双随机矩阵积和式下界的一个估计，若一个n×n矩阵A的每个分量都是非负的，而且每个行和与每个列和都等于1，则称A是一个双随机矩阵，设A为一个双随机矩阵，范·德·瓦尔登猜想是per A≥n!/nn，并且等号成立当且仅当A的每个元素均为1/n。此猜想于1980年被苏联学者埃果里切夫(Г.П.Егорычев)所证实，其证明采用了其他数学家的一系列结果1。

基本介绍范·德·瓦尔登(Van der Waerden)猜想是组合数学中关于正项行列式的一个极为重要的猜想。

设A是一个n行n列的矩阵，元素是aij，A的积和式定义为

求和遍及(1，2，…，n)的一切排列σ，其中，Sn表示n个符号的对称群，A称为双随机矩阵，是指它的每一行元素的和，每一列元素的和都等于1，则Jn是每个阵元都是的双随机矩阵。

在1927年，范·德·瓦尔登猜测：对于双随机矩阵A，成立着不等式

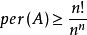等号当且仅当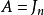，即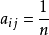时成立，这里。这一猜测直到1984年前不久才被证明2。

相关说明1959年，马库斯和纽曼发表了关于范·德·瓦尔登猜想的第一篇论文，他们证明了在所有双随机矩阵的集合上，Jn是正项行列式函数的局部极小点，他们推导出使其正项行列式达到极小的双随机矩阵应满足的性质，并对n=3的情形证明了这个猜想，此后，许多数学家写了大量的文章对于n=4，n=5的情形。以及对许多特殊的类型的双随机矩阵证明了这个猜想3。

在另一个方向上，班于1976年，而弗里德兰(S.Friedland)于1979年彼此独立地证明了对于任何双随机矩阵A有：

这个结果并不比范·德·瓦尔登的猜想弱多少，因为由斯特灵公式，近似等于。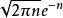

现在范·德·瓦尔登猜想已经由两位前苏联数学家独立地解决了，一位是乌克兰共和国建筑业计划与管理自动系统科学研究所的法利克曼(D.I.Falikman)，另一位是基雷斯基克拉斯诺雅茨克的苏联科学院西伯利亚分院的基雷斯基(L.V.Kirensky)物理研究所的埃戈里奇夫(G.P.Egorychev)。从时间上看是法利克曼先得到其证明，他早在1979年5月就把他的论文投寄给《数学注记》，而埃戈里奇夫一直到1980年末才散发他的论文的预印本，但法利克曼只是证明了范·德·瓦尔登定理，而埃戈里奇夫，另外还得到更强的结果：Jn是唯一的使正项行列式达到极小的双随机矩阵，虽然他们的证明在细节上有所差别，但都应用了亚历山大德诺夫在1938年得到的一个关于二次型的混合判别式的不等式的特殊情形。

正如拉盖里阿斯(J.C.Lagarias)所指出的那样，范·德·瓦尔登猜想是一个富有挑战性的问题，但是，这问题的解决并没有给数学知识的现状带来革命性的变化，而要是黎曼猜想得到证明则肯定会这样，然而，范·德·瓦尔登猜想肯定可以得出比以前更好的互不同构的拉丁方和斯坦纳(Steiner)三元系的数目的下界，从长远观点看来，最有意义的结果是从关于二次型的混合判别式的亚历山大德诺夫不等式以及与此有关的关于凸体的混合体积的亚历山大德夫一芬切尔不等式可以推出大量的具有有趣组合解释的多重线性不等式3。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学