[科普中国]-补设计

补设计(complementary design)是由一个区组设计派生的另一个区组设计，若一个区组设计(X，B)的区组为B1，B2，…，Bb，对每个区组Bi，做B′i=X\Bi，把这样得到的所有B′i作为区组族B′，则称(X，B′)为区组设计(X，B)的补设计1。

基本介绍若一个区组设计(X，B)的区组为B1，B2，…，Bb，对每个区组Bi，做B′i=X\Bi，把这样得到的所有B′i作为区组族B′，则称(X，B′)为区组设计(X，B)的补设计。一个(v，b，r，k，λ)-BIBD的补设计是一个(v，b，b-r，v-k，b-2r+λ)-BIBD，若区组设计(X，B)的关联矩阵为A，则其补设计的关联矩阵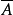 =Jb×v-A，这里Jb×v是元素全为1的b×v矩阵1。

相关介绍m×n的(0，1)矩阵A=(aij)的补矩阵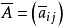 是指满足条件

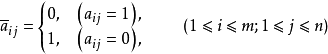的m×n的(0，1)矩阵，矩阵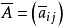也称为(A1，A2，…，Am)限位排列的关联矩阵A的补，与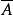相应的限位排列问题，称为原限位排列问题的补问题。一个限位排列问题的补问题与一个车问题相对应。

关联矩阵(1)的补是

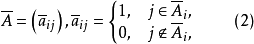对待矩阵(2)可有两种观点。第一，可把(2)看作某一个限位排列问题——称为原限位排列问题的补问题——的关联矩阵，其限制条件正好是原限制条件的补：

元j的限位集为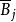，禁位集为Bj；

第i位的限元集为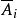，禁元集为Ai.

第二，可以把(2)看作一个棋阵，它由一个m×n的矩形棋盘上的mn个格子组成，每个格子要么是1，要么是零；把有1的格子称为实格，其他格子称为虚格。

如果约定，在棋阵的实格处不允许放上棋子，那么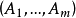，-限位排列问题就化为，寻求在棋阵(2)上放置m个互不相遇的棋子的放法的个数。这里，所谓二个棋子相遇，意指它们在棋盘上的同一行或同一列2。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学