哈密顿-雅可比-贝尔曼方程(Hamilton-Jacobi-Bellman equation,简称HJB方程)是一个偏微分方程,是最优控制的核心。HJB方程式的解是针对特定动态系统及相关代价函数下,有最小代价的实值函数。
简介哈密顿-雅可比-贝尔曼方程(Hamilton-Jacobi-Bellman equation,简称HJB方程)是一个偏微分方程,是最优控制的核心。HJB方程式的解是针对特定动态系统及相关代价函数下,有最小代价的实值函数。
若只在某一个区域求解,HJB方程是一个必要条件,若是在整个状态空间下求解,HJB方程是充份必要条件。其解是针对开环系统,但也允许针对闭环系统求解。HJB方程也可以扩展到随机系统。
一些经典的变分问题,例如最速降线问题,可以用此方法求解。
HJB方程的基础是以1950年代由理查德·贝尔曼及其同仁提出的动态规划。对应的离散系统方程式一般称为贝尔曼方程。在连续时间的结果可以视为由卡尔·雅可比及威廉·哈密顿提出,经典力学中哈密顿-雅可比方程的延伸。1
最佳控制的问题考虑在时间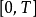 内,以下确定系统最佳控制的问题:
内,以下确定系统最佳控制的问题:
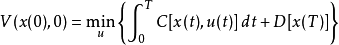 其中C[ ]为标量成本函数,D[ ]为计算其最终状态时效力时或经济值的函数,x(t)为系统状态向量,x(0)假设已知,及u(t)是想要求得的控制向量,在 0≤t≤T。
其中C[ ]为标量成本函数,D[ ]为计算其最终状态时效力时或经济值的函数,x(t)为系统状态向量,x(0)假设已知,及u(t)是想要求得的控制向量,在 0≤t≤T。
此系统也需满足下式:
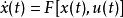 其中F[ ]可以根据状态向量决定向量后续的变化。1
其中F[ ]可以根据状态向量决定向量后续的变化。1
微分方程对于一个简单系统,哈密顿-雅可比-贝尔曼微分方程是:
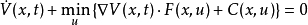
它的边界条件是: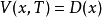
这里的 指
指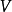 关于时间变量
关于时间变量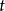 的导数,
的导数,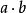 表示向量a,b的点乘,
表示向量a,b的点乘,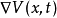 是
是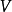 关于变量
关于变量 的梯度。
的梯度。
在上述微分方程中,未知标量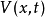 被称为贝尔曼价值函数,代表了系统从时间
被称为贝尔曼价值函数,代表了系统从时间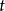 时的状态开始,按照最优路径控制,直到时间
时的状态开始,按照最优路径控制,直到时间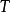 时的价值消耗。
时的价值消耗。
方程推导我们可以这样得到HJB方程。
如果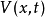 是一个代价函数(或者称其为贝尔曼价值函数),那么根据理查德·贝尔曼的最优性原理,从时间t到t+dt,我们可以得到:
是一个代价函数(或者称其为贝尔曼价值函数),那么根据理查德·贝尔曼的最优性原理,从时间t到t+dt,我们可以得到:
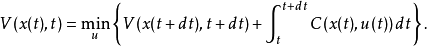
我们可以注意到,对右边公式第一项做泰勒展开,可以得到:
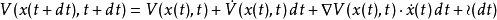
这里的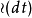 表示在泰勒展开中,高于1阶的无穷小量。如果两边同时消去
表示在泰勒展开中,高于1阶的无穷小量。如果两边同时消去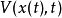 ,同时除去dt,当dt趋向于0时,对式子取极限,我们就能得到哈密顿-雅可比-贝尔曼(HJB)方程。
,同时除去dt,当dt趋向于0时,对式子取极限,我们就能得到哈密顿-雅可比-贝尔曼(HJB)方程。
相关条目贝尔曼方程,离散的哈密顿-雅可比-贝尔曼方程。
Pontryagin最小值定理,是将哈密顿量最小值,是最佳化必要但不充份的条件,和哈密顿-雅可比-贝尔曼方程相比的好处是只要考虑满足条件的单一轨迹。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国