[科普中国]-棋盘完全覆盖问题

棋盘完全覆盖问题(problem of perfect cover of chessboard)是一类组合问题，一个8×8国际象棋棋盘，m×n广义棋盘，以及任意形式的残破棋盘都可以被骨牌覆盖。棋盘的一个完全覆盖是若干骨牌安排到棋盘上，使：1.每块骨牌覆盖棋盘上相邻两格；2.棋盘上每一格都被骨牌覆盖；3.没有两块骨牌同时覆盖一格1。

问题总述考虑一个普通的棋盘，它有8行和8列，总共分成64个方格，设一个方格是1 cm2，问能否用32张长2 cm，宽1cm的纸片将棋盘覆盖住(任两片纸片不重叠且不能将纸片剪断)，这个问题称为棋盘的完全覆盖问题，显然很容易作出许多不同的完全覆盖，要计算不同的完全覆盖的个数虽然是困难的，但仍可算出来。1961年M.E.Fischer发现这个数是12988816=24×(921)2。2

m×n棋盘的完全覆盖以上问题可推广到m行n列，mn个方格的棋盘的覆盖问题，也可以表述为：用2×1的骨牌，去覆盖一张m×n的棋盘，使得每一个骨牌占两个方格，而每个方格都有骨牌占住，而且没有两块骨牌重叠。

此时完全覆盖就未必存在，如3×3棋盖就不能完全覆盖。那么对于m和n的哪些值，m×n的棋盘有完全覆盖呢?不难看到，一个m×n的棋盘有完全覆盖的充要条件是m和n至少有一个是偶数，换句话说，棋盘中的方格的个数是偶数3。

对于m×n棋盘的覆盖，最为困难的问题要算对覆盖种数的讨论。

假定我们用F(m，n)表示m×n棋盘覆盖方式的总数，显然，我们有

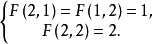当n≥3时，读者不难从下图看出

F(2，n) =F(2，n-1)+F(2，n-2).

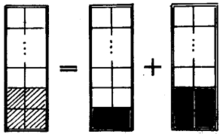
由此可以推得数列{F(2，n)}如下；

1， 2， 3， 5， 8，13，21， 34， 55，．．．．．

聪明的读者想必都知道，这是著名的菲波那契数列!

至于求F(m，n)的一般公式，那是一项异常艰巨的工作。只知道公元1961年，M.E.费切尔求出8×8棋盘的覆盖方式的总数为

F(8，8)=24×(901)2=12988816.

其难度可想而知3。

残缺棋盘的完全覆盖把一个棋盘随意剪去一些方格，得到的是一张“残缺棋盘”。那么，关于残缺棋盘的覆盖问题又怎么样呢?

当然，在残缺棋盘上留下的方格必须是偶数个，否则根本谈不上覆盖。但并不是所有偶数方格的残缺棋盘都能覆盖得了，下图3就是一个有启迪性的例子。那是一张去掉两个角的国际象棋棋盘，它不可能用两方格的多米诺骨牌去覆盖。事实上，我们可以把多米诺骨牌看成是由一个白格和一个黑格组成。很明显，凡能用多米诺

骨牌覆盖的棋盘，其黑格与白格一定一样多，然而图上的残缺棋盘少了二个白格显然不满足这个要求。

读者试一试就会发现，下面两张各挖去一个方格的3×5残缺棋盘，一个是可以覆盖的(图4(Ⅰ))，而另一个却不能覆盖(图4(Ⅱ))。那么，其中的奥妙在哪里呢?

原来，被挖掉的方格的位置有讲究。如果我们将上图像国际象棋盘那样把方格黑白相间涂色，那么这一点将会看得更清楚。例如，上图Ⅱ中白格原本就少，而现在挖去的又是白格，致使黑格比白格净多两个，自然就更无法覆盖了!

再考虑一个8×8棋盘用剪刀剪掉对角上两个方格，能否放置31张纸片把这个残缺的棋盘完全覆盖呢?我们对8×8棋盘上的方格用黑白交替着色，共有32个黑色方格和32个白色方格，如果我们剪掉对角上的两个方格，我们就剪掉了两个同样颜色的方格，比方说是白色的，这样就剩下32个黑色方格和30个白色方格，因此31张纸片必定覆盖棋盘上31个黑色方格和31个白色方格，因此对这个残缺棋盘不能用31张纸片完全覆盖2。

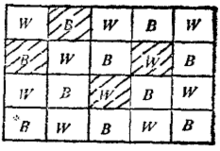
更一般地说，可以取一个黑白交替着色的m×n棋盘，并且任意剪掉若干方格，什么样的残缺棋盘有完全覆盖呢?由上面所述知，残缺棋盘具有完全覆盖的必要条件是黑白方格的个数相同，不过如图5、6所示，这个条件并不是充分条件2。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学