[科普中国]-t设计

t设计(t-design)是平衡不完全区组设计的一种推广，设D=(V,B)为有限关联结构，若下列条件满足：(i)|V|=v；(ii)存在常数k，使对所有B∈B，都有kB=k；(iii)对给定的正整数t，存在常数λ>0，使对V的任意一个t元子集S，都有λs=λ，则称D为一个t-(v,k,λ)设计，简称t-设计，t-(v,k,λ)设计常记作Sλ(t，k；v)。设D=(V，B)为一个t-(v,k,λ)设计，如果V的每个k元子集都在B中出现相同的次数，则称D为平凡的t-设计。例如当v≤k+t时，任一t-(v,k,λ)设计都是平凡的1。

基本介绍设(X，B)为一正则设计(参见“区组设计”)，其中|X|=v，区组大小为k，若X的任一t元子集恰含于B的λ个区组之中，则称(X，B)为t-(v，k，λ)设计，简称t设计，一个2-(v，k，λ)设计就是(v，k，λ)-BIBD，没有重复区组的t设计称为简单t设计，λ=1的t-(v，k，λ)设计称为施泰纳系，记为S(t，k，v)，从而t设计有时也记为Sλ(t，k，v)。

一个t-(v，k，λ)设计也是一个s-(v，k，λs)设计，式中

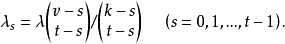这提供了t设计参数t，v，k，λ应满足的必要条件：

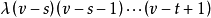
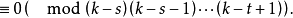这些参数还必须满足推广的费希尔不等式,若(X，B)是一个t-(v，k，λ)设计，并且|B|=b，则当t=2s且v≥k+s时，

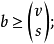当t=2s+1且v≥k+s+1时，

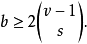
若X的每个k元子集在B中出现相同次数，则称t设计(X，B)是平凡的。例如，v元集X的全体k元子集构成一个平凡的t设计，泰尔林克(L.Teirlink)证明：对所有t都存在非平凡的简单t设计，威尔森(R.W.Wilson)指出：当λ充分大时，上述关于t-(v，k，λ)设计存在的必要条件也是充分的。哈拿匿(H.Hanani)得到了3-(v，4，λ)设计存在性的完整结果：3-(v，4，λ)设计存在的充分必要条件是：

λ(v-2)≡0(mod 2)，

λ(v-1)(v-2)≡0(mod 3)

且λv(v-1)(v-2)≡0(mod 8)；对其他参数情形，目前很少有完整结果2。

t-设计的若干特殊类型下面给出t-设计的若干特殊类型：

(i)t=1，1-设计也叫战术构形(tactical configuration)或构形。

(ii)t=2，2-设计即熟知的BIB设计，2-(v，k，λ)设计通常记作B(k，λ；v)。

(iii)k=t，λ=1，t-(v，t，1)设计也叫完全超图(complete hypergraph)。

k=t=2时。2-(v，2，1)设计叫完全图(complete graph)。

(iv)λ=1，t-(v，k，1)设计常叫做Steiner系。并记作S(t，k，v)。

(v)Sλ(2，3，v)叫三元系，特别，S(2,3,v)叫Steiner三元系，记作STS(v)。

(vi)Sλ(3，4，v)叫四元系(quadruple system)，特别，S(3，4，v)叫做Steiner四元系，记作SQS(v)。1

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学