[科普中国]-近似极限

近似极限是普通极限概念的一种推广。对一切以x0为全密点的点集E，下（上）确界称为f(x)在点x0的近似上（下）极限。

简介近似极限是普通极限概念的一种推广，对一切以x0为全密点的点集E，下（上）确界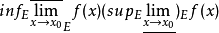称为f(x)在点x0的近似上（下）极限，记为

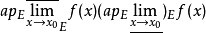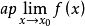若，记为。1

推论由近似极限可知以下命题成立：

1、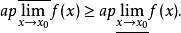

2、设x0为E的全密点，若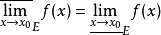，则。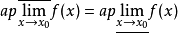

3、若f(x)在点x0有有限的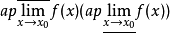则存在以x0为全密点的点集E，使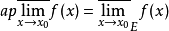或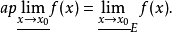

4、（A为有限数）的充分必要条件为存在以x0为全密点的点集E，使

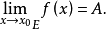
极限“极限”是数学中的分支——微积分的基础概念，广义的“极限”是指“无限靠近而永远不能到达”的意思。数学中的“极限”指：某一个函数中的某一个变量，此变量在变大（或者变小）的永远变化的过程中，逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”（“永远不能够等于A，但是取等于A‘已经足够取得高精度计算结果）的过程中，此变量的变化，被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近A点的趋势”。

极限是一种“变化状态”的描述。此变量永远趋近的值A叫做“极限值”（当然也可以用其他符号表示）。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学