[科普中国]-简单曲线

在平面上确定一条连续曲线γ，若对任意的t1∈(a,b)及t2∈[a,b]，只要t1≠t2就有z(t1)≠z(t2)，则称连续曲线γ为简单曲线或若尔当弧。

定义连续曲线连续曲线是复平面上的拓扑基本概念之一。闭线段a≤t≤b(a≠b)到复平面的连续映射称为连续曲线。若x(t)和y(t)是两个在区间a≤t≤b上连续的函数，则

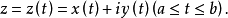
简单曲线在平面上确定一条连续曲线γ，若对任意的t1∈(a,b)及t2∈[a,b]，只要t1≠t2就有z(t1)≠z(t2)，则称连续曲线γ为简单曲线或若尔当弧。

z(a)称为这条简单曲线的起点，z(b)称为这条简单曲线的终点。1

简单闭曲线若简单曲线γ还满足z(a)=z(b)，则称γ为简单闭曲线。简单闭曲线也称为若尔当曲线。

简单来说，平面上一条连续的简单曲线就叫做若尔当曲线。

以一条简单闭曲线C为公共边界可把平面分成两个区域：一个是有界的，称为C的内部，另一个是无界的，称为C的外部。

实例简单曲线是平面上的一个有界闭集。例如，线段、圆弧和抛物线等都是简单曲线。

圆周和椭圆周等都是简单闭曲线。2

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学