波尔查诺-魏尔施特拉斯定理是数学拓扑学与实分析中用以刻划中的紧集的基本定理,得名于数学家伯纳德·波尔查诺与卡尔·魏尔施特拉斯。
简介波尔查诺-魏尔施特拉斯定理是数学拓扑学与实分析中用以刻划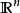 中的紧集的基本定理,得名于数学家伯纳德·波尔查诺与卡尔·魏尔施特拉斯。波尔查诺-魏尔斯特拉斯定理说明,有限维实向量空间
中的紧集的基本定理,得名于数学家伯纳德·波尔查诺与卡尔·魏尔施特拉斯。波尔查诺-魏尔斯特拉斯定理说明,有限维实向量空间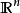 中的一个子集E是序列紧致(每个序列都有收敛子序列)当且仅当E是有界闭集。1
中的一个子集E是序列紧致(每个序列都有收敛子序列)当且仅当E是有界闭集。1
历史这个定理最早由伯纳德·波尔扎诺证明,当他在证明介值定理时,附带证明了这个定理,但是他的证明已经散佚。卡尔·魏尔施特拉斯独自发现并证明了这个定理。波尔扎诺-魏尔施特拉斯定理是实分析中的基本定理。1
基础概念子列:也称为子序列。一个序列 的一个子列是指在
的一个子列是指在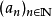 中抽取无穷多个元素,然后按照它们在原来序列里的顺序排列起来的序列。严格的定义是:如果存在一个从
中抽取无穷多个元素,然后按照它们在原来序列里的顺序排列起来的序列。严格的定义是:如果存在一个从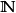 到
到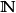 的严格单调递增的映射
的严格单调递增的映射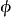 ,使得
,使得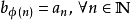 ,就称
,就称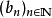 是
是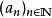 的一个子列。
的一个子列。
有界闭集: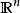 中的有界闭集概念建立在给定的拓扑和度量上的。由于在有限维向量空间中所有度量等价,所以可以将
中的有界闭集概念建立在给定的拓扑和度量上的。由于在有限维向量空间中所有度量等价,所以可以将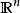 视为装备了欧几里德度量的度量空间(并且可以定义相应的范数)。
视为装备了欧几里德度量的度量空间(并且可以定义相应的范数)。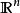 的子集E有界,当且仅当所有E中元素x的范数小于一个给定常数K。注意这时对应的拓扑是欧几里德范数诱导的自然拓扑。
的子集E有界,当且仅当所有E中元素x的范数小于一个给定常数K。注意这时对应的拓扑是欧几里德范数诱导的自然拓扑。
序列紧致:称一个集合S是序列紧致的,是指每个由集合S中元素所组成的数列都包含收敛的子列,并且该子列收敛到集合S中的某个元素。1
波尔查诺-魏尔斯特拉斯性质在有限维度量空间中,波尔查诺-魏尔斯特拉斯说明了序列紧致的集合就是有界闭集。然而在一般的度量空间中,有界闭集不一定是序列紧致的。为此,拓扑学中将一般度量空间中的序列紧致称为波尔查诺-魏尔斯特拉斯性质。
定义:
设K为度量空间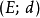 的子集。若K中任一序列
的子集。若K中任一序列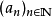 都包含一个收敛的子列,其极限也是K中元素,就称K具有波尔查诺-魏尔斯特拉斯性质。
都包含一个收敛的子列,其极限也是K中元素,就称K具有波尔查诺-魏尔斯特拉斯性质。
如果度量空间本身满足波尔查诺-魏尔斯特拉斯性质,就称这个度量空间为紧空间。在度量空间中,波尔查诺-魏尔斯特拉斯性质等价于海恩-波莱尔性质:所有K的开覆盖都有限子覆盖。1
本词条内容贡献者为:
任毅如 - 副教授 - 湖南大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国