谐波小波转换(Harmonic Wavelet Transform)为学者大卫‧纽兰德(David E. Newland)于1993年所提出,是一个以小波为基底的线性转换,得以将信号变换至时频域(Time-Frequency Domain)上。谐波小波转换结合了短时距傅立叶变换和连续小波转换两者之优点的信号分析工具,而其离散版本则可以用快速傅立叶变换做有效率的运算。
基础推理考量一个偶对称的实数函数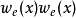 ,其傅立叶变换定义为:
,其傅立叶变换定义为:
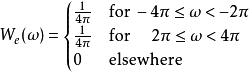
则透过反傅立叶变换,我们可以得到该函数 {\displaystyle w_{e}(x)} {\displaystyle w_{e}(x)}为:
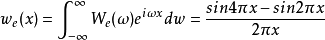
而考量另一奇对称的函数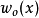 ,若定义其傅立叶变换为:
,若定义其傅立叶变换为:
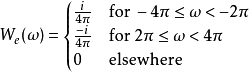
则其反傅立叶变换会得到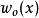 为:
为:
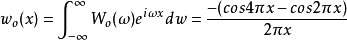
假如结合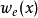 和
和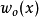 ,透过
,透过 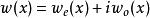 的关系,我们会得到一复数函数,并定义它为谐波小波(Harmonic Wavelet)。本谐波小波将为以下数学形式:
的关系,我们会得到一复数函数,并定义它为谐波小波(Harmonic Wavelet)。本谐波小波将为以下数学形式:
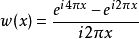
也由于傅立叶转换的特性和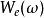 },
}, 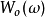 的定义,谐波小波的傅立叶转换对为:
的定义,谐波小波的傅立叶转换对为:

一系列的谐波小波接着,考量到小波转换中的精神--母小波的缩放(Dilation)和平移,透过伸张方程式(Dilation Equation)我们可以写出一系列的谐波小波(其中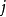 和
和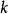 皆为整数):
皆为整数):
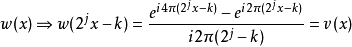
根据前文对 的定义,或是透过直接计算傅立叶转换对,我们也可以得到缩放和平移后的一系列谐波小波在频域上的表示法:
的定义,或是透过直接计算傅立叶转换对,我们也可以得到缩放和平移后的一系列谐波小波在频域上的表示法:
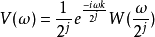
而若我们将不同的正整数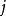 带入上式,例如
带入上式,例如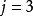 和
和 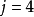 ,我们会发现后者的振幅会是前者的一半,然而其频带宽会是前者的两倍。这样的特性使得每一阶(Level,对应到不同的
,我们会发现后者的振幅会是前者的一半,然而其频带宽会是前者的两倍。这样的特性使得每一阶(Level,对应到不同的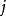 )的谐波小波,其频域将随着阶数越高而越宽,由是达到多分辨率的效果1。
)的谐波小波,其频域将随着阶数越高而越宽,由是达到多分辨率的效果1。
低频频带与正交随着 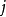 的阶数比0越来越小,频带的振幅将越来越高、越来越窄,一路向频率为0的位置延伸。而根据多分辨率分析的理论,我们可以将这些阶数小于0的频带全部收为一个频带,并定义为-1阶(
的阶数比0越来越小,频带的振幅将越来越高、越来越窄,一路向频率为0的位置延伸。而根据多分辨率分析的理论,我们可以将这些阶数小于0的频带全部收为一个频带,并定义为-1阶(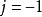 )。它涵盖了DC到
)。它涵盖了DC到 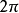 的频带范围。以小波转换的术语来说,这样具低通滤波性质的函式,被称之为缩放函数(Scaling Function),又称为父小波(Father Wavelet)。谐波小波的缩放函数定义为:
的频带范围。以小波转换的术语来说,这样具低通滤波性质的函式,被称之为缩放函数(Scaling Function),又称为父小波(Father Wavelet)。谐波小波的缩放函数定义为:
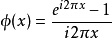 ,其频域特性将是一个介于
,其频域特性将是一个介于 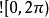 的方波,振幅为
的方波,振幅为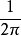
若要证明谐波小波有正交的特性,必须分两个层次讨论, (不同阶的谐波小波)和
(不同阶的谐波小波)和 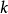 (不同位移量)。首先讨论不同阶的谐波小波。根据傅立叶理论,若两任意阶数的谐波小波正交,它将有下列关系(参考David Newland,1993):
(不同位移量)。首先讨论不同阶的谐波小波。根据傅立叶理论,若两任意阶数的谐波小波正交,它将有下列关系(参考David Newland,1993):
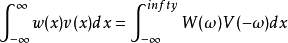
因为任意阶数之谐波小波其频谱皆分布在正频率轴,故 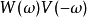 永远为0。我们还必须证明下式也成立:
永远为0。我们还必须证明下式也成立:
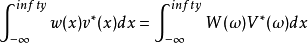
而因为不同阶数之谐波小波其频带不相交,故上式的右式也为0,由是证明不同阶数谐波小波的正交特性。至于同阶数、不同位移量的谐波小波,因为傅立叶变换的特性,在时域的位移相当于在频域的讯号必须乘上一个线性相位,因此对位移之谐波小波来说,必须满足下式:
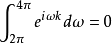
当k不为0的时候,上式将会成立。换言之,当具有位移存在时,谐波小波正交的特质成立。最后,我们也可以用相似的证明方式,证明谐波小波之父小波也具有正交特性。
短时距傅里叶变换与连续小波转换短时距傅里叶变换是傅里叶变换的一种变形,用于决定随时间变化的信号局部部分的正弦频率和相位。实际上,计算短时傅里叶变换(STFT)的过程是将长时间信号分成数个较短的等长信号,然后再分别计算每个较短段的傅里叶变换。通常拿来描绘频域与时域上的变化,为时频分析中其中一个重要的工具。
连续小波转换(Continuous Wavelet Transform)是一种用来分解一个连续时间函数,使它变成数个小波(wavelet)。跟傅里叶变换(Fourier Transform)不一样的是,连续小波转换可以建构一个具有良好时域和频域局部化的时频讯号。以数学来说,一个有连续时间性质且可积分的函数 可以用下面的积分来表示
可以用下面的积分来表示
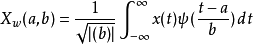
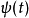 为小波母函数(Mother Wavelet),一个在时间领域和频率领域都有连续性质的函数,
为小波母函数(Mother Wavelet),一个在时间领域和频率领域都有连续性质的函数, 为平移位置而
为平移位置而  为缩放因子。小波母函数的用途在于提供一个可以产生子波(Daughter Wavelet)的根源函数,而子波是小波母函数平移过或缩放过(或两者都有)的版本。如果要将已知且存在的讯号
为缩放因子。小波母函数的用途在于提供一个可以产生子波(Daughter Wavelet)的根源函数,而子波是小波母函数平移过或缩放过(或两者都有)的版本。如果要将已知且存在的讯号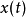 恢复原来的形式,我们可以用反转连续小波转换(Inverse Continuous Wavelet Transform)
恢复原来的形式,我们可以用反转连续小波转换(Inverse Continuous Wavelet Transform)
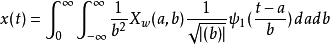
 为
为 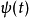 的双效函数(Dual Function)。 而这个双效函数必须满足
的双效函数(Dual Function)。 而这个双效函数必须满足
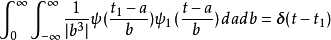
本词条内容贡献者为:
何星 - 副教授 - 上海交通大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国