艾克纳方程是质量守恒的定理,是有关河流中沉积物的质量守恒。
简介艾克纳方程是质量守恒的定理,是有关河流中沉积物的质量守恒1。最早是由奥地利气象学家及沉积物学家费利克斯·马力亚·埃克斯纳开始研究,2艾克纳方程因此而得名。
方程式艾克纳方程描述河流在河流作用下,沉积物搬运过程的质量守恒定理.河底的高度会随累积的沉积物而渐渐增加(河流淤积),会因沉积物随着河流清出而渐渐下降(陵夷作用)。
基础方程式此方程提到河床高度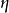 随着时间t的变化,等于沉积物通量散度的负值,除以颗粒填集密度(grain packing density)
随着时间t的变化,等于沉积物通量散度的负值,除以颗粒填集密度(grain packing density)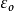 的结果:
的结果:
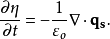 其中
其中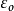 可以表示为
可以表示为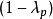 ,其中
,其中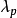 为河床的孔隙率。
为河床的孔隙率。
自然界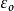 的范围约在0.45 至0.75之间,若是球形颗粒依随机密堆积的方式堆积,其数值约为 0.64,密堆积的上限为0.74048(参照最密堆积),但在自然界不太可能以最密堆积的方式堆积,因此多半是用随机密堆积的方式进行,这也是较合理的上限。
的范围约在0.45 至0.75之间,若是球形颗粒依随机密堆积的方式堆积,其数值约为 0.64,密堆积的上限为0.74048(参照最密堆积),但在自然界不太可能以最密堆积的方式堆积,因此多半是用随机密堆积的方式进行,这也是较合理的上限。
一维的艾克纳方程常会因为计算的方便或/及缺乏相关资料而出现。一般以是往下游的方向x为准,因为一般关注的也是随着河流往下,河流的侵蚀作用及堆积作用。
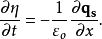
包括高度因外力变化的方程式此情形下的艾克纳方程会在质量守恒式子中包括地层下陷的项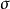 ,这允许在河床高度因外在因素影响时,计算河床的绝对高度
,这允许在河床高度因外在因素影响时,计算河床的绝对高度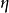 对时间的变化,外在因素可能是地质构造或是地壳均衡造成的高度变化,若河床高度随时间增加,
对时间的变化,外在因素可能是地质构造或是地壳均衡造成的高度变化,若河床高度随时间增加,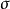 为正值,若河床高度随时间减少增加,
为正值,若河床高度随时间减少增加,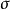 为负值。
为负值。
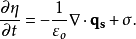
重要性艾克纳方程的重要性在于水深与斜度会影响其剪应力,从而引起地区侵蚀及堆积作用。
本词条内容贡献者为:
张尉 - 副教授 - 西南大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国