[科普中国]-卡拉西奥多里条件

卡拉西奥多里条件是用以定义勒贝格可测集的一个条件。这一条件是卡拉西奥多里(Caratheodory,C.)于1914年首先提出的，它在非线性积分算子理论和各种非线性问题中，起着重要的作用。

简介卡拉西奥多里条件是用以定义勒贝格可测集的一个条件。

这一条件是卡拉西奥多里(Caratheodory,C.)于1914年首先提出的，它在非线性积分算子理论和各种非线性问题中，起着重要的作用。

发展对有界闭集F⊂(a,b)，令G=(a,b)\F，定义F的测度为m(F)=(b-a)-m(G)，m(F)与区间(a,b)的选择无关；

对一般的有界点集E，把所有包含E的有界开集的测度的下确界称为E的外测度，记为m*(E)，即m*(E)=inf{m(G)|G为开集且G⊃E}；把所有包含E的有界开集的测度的上确界称为E的（勒贝格）内测度，记为m*(E)或|E|i，即m*(E)=sup{m(F)|F为闭集且F⊃E}；显然，m*(E)≤m*(E)；若m*(E)=m*(E)，则称E为可测集，它的外测度与内测度所具有的共同值称为E的测度，记为m(E)=m，(E)=m*(E)。

若E为无界集，且它与任何有界开区间的交是可测集，则称E是可测集，其测度定义为

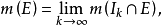其中{Ik}为递增开区间列，且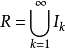，而且m(E)可能为+∞。

以上关于R中点集的可测集与测度的概念可以推广到Rn中的点集上去，而且这种推广并无实质性的困难。

应用勒贝格可测集与测度的优点是自然、直观，然而定义中使用了内测度与外测度，这样，使用起来很不方便。因此人们希望寻求一个比较简洁的等价定义。

通过对外测度的深入研究，卡拉西奥多里于1914年给出了前面所述的可测集的定义，这个定义与勒贝格的定义是等价的，而且后来成为建立抽象测度论的有力工具。1

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学