[科普中国]-弱序关系

弱序关系(weak-ordering relation)亦称弱优选关系，是一种重要的二元关系，指集合A中的自反的、传递的、连通的二元关系R。弱序关系R对任何a，b∈A，有aRb或bRa，A称为弱序集，全序是一种弱序，弱序若还是反对称的，则就是全序。弱序集虽然是强连通的，但一般不能排成一行1。

基本概念所谓的二元关系(Binary Relation)是指，将两个事物联系在一起的某种特征，例如：

a是b的兄弟

c位于d的左方

e比f大

g偏好(优)于h

i等于j

我们可以在上述字母之间放置某种符号来表示它们之间所存在的二元关系,例如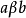可以表示“a是b的兄弟”。在定义该关系时，必须先定义该关系是在什么样的域(Domain)上被定义。

下面将给出一些非常有用的定义。

自反性(Reflexivity) 令R表示定义在集合S上的一个关系，若对所有的x∈S，有xRx，则称关系R为自反的。若定义关系域中的所有元素都可将此关系返回其自身，则该关系是自反的。例如，相等关系(=)就是自反的。

传递性(Transitivity) 若xRy和yRz蕴涵xRz，则称二元关系R为传递的。例如，相等关系就是传递的，在由实数R构成的集合中,大于关系(>)也是传递的。

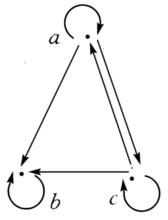
弱序(Quasi-orderings) 一个具有自反性和传递性的二元关系称为一个弱序。可以选用任意一个方便的标记符号来表示一个弱序关系。表示弱序的常用符号是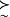。在由实数R构成的集合中。大于或等于关系(≥)就是一个典型的弱序关系。如下面的箭头图表示集合A={a，b，c}上的关系R是弱序，既非全序又非偏序，因为有aRc，cRa，但a≠c。

关系的完备性 只是定义在集合S上的一个关系，若对每一x，y∈S，xRy或yRx关系成立，或者有两种关系同时成立，则称关系只是完备的。若关系R按一个方向；或另一相反方向，或同时两个方向定义了集合S中元素构成的所有序偶之间的相互关系，则定义在集合S上的关系只是完备的。若关系R对由集合S中元素构成的所有序偶都有定义，则关系只是完备的2。

弱序的上界弱序的上界(UpperBound) 令集合S已被弱序关系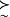定义；令X⊂S，若存在y∈S

满足任一x∈X，y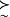x，则称y是x的一个上界。令Y={y|y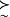x，所有x∈X}，若存在y’∈Y满足所有y∈Y，y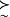y'，则称y'为X的最小上界。

请读者注意，无论何时，只要X⊂R有一个上界，则X总有一个最小上界，这是有弱序(≥)定义的实数R所具有的一个性质2。

弱序的等值集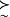的上等值集(UpperContour Set) 令集合S已被弱序关系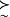定义，从任意一点y∈S开始，在弱序关系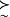下优于y的点可以构成一个集合，则该集合称为y的上等值集：A(y)={x|x∈S，x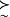y}。

相似地，可以定义在弱序关系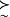下y的下等值集。

在弱序关系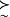下，所有次于y的点构成的集合称为y的下等值集：G(y)={x|x∈S，y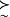x}。

当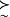表示一个偏好序时，这就是大家熟悉的对无差异曲线的一个排序。穿过y的无差异曲线可以表示为{x|x∈S，x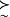y且y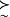x}=A(y)∩G(y)2。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学