[科普中国]-部分平衡不完全区组设计-

设v元集S上有m个结合关系Ri(1≤i≤m)的结合方案，且S上的一个区组设计有b个区组，若每个区组大小为k，S中任一元恰在r个区组中出现，并且任意两个有第i种结合关系的元恰同时出现在λ个区组之中，则称该区组设计是一个具有m个结合类的PBIBD设计。

结合方案若S={s1,s2,...,sv}为一v元集，且(S×S)\{(s,s)}s∈S}可表为m个两两不相交的非空子集R1,R2,...,Rm的并，则称R为结合关系。若诸关系Ri满足：

1.每一关系Ri是对称的，即当(x,y)∈Ri时，必有(y,x)∈Ri。

2.对S中的每个元x，与x有第i种结合关系的元y的个数，即|{y∈S|(x,y)∈Ri}|川只依赖于i，与x的具体选择无关，此数记为ni。

3.设x,y有第i种结合关系，则与x有第j种结合关系且与y有第k种结合关系的元z的个数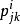只依赖于数i，j，k，而与x，y的具体选择无关，则称集S连同诸关系Ri为一个具有m个结合类（或关系）的结合方案。诸数v，ni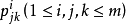，称为该结合方案的参数。基集S的元称为处理。

简介部分平衡不完全区组设计是平衡不完全区组设计的一种推广，简记为PBIBD。它是基于结合方案的概念，最早由玻色(Bose,R.C.)及内尔(Nair,K.R.)于1939年提出。

诸数b，v，r，k，λi，ni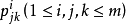，称为PBIBD设计的参数。当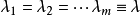时，PBIBD设计就是一个(v,k,λ)-PBIBD。

分类按结合方案的类型，具有两个结合类的PBIBD设计可分为可分组PBIBD设计、三角形设计、拉丁方型设计等，利用有限域上向量空间以及利用多种有限几何（辛几何、酉几何、正交几何等）构造结合方案和相应PBIBD设计在中国有比较活跃的研究，它起源于班成的工作，而万哲先等人则做了较为系统的研究。

应用在试验设计中，PBIBD设计被用来安排试验的方案，其中有两个结合类且参数较小的PBIBD设计最为有用，它们的存在性及构造已有表可查。结合方案与一类结合的交换代数有关，称为结合方案的玻色-梅斯纳代数，最重要的一类结合方案与编码理论有关，称为汉明结合方案。另一类结合方案与强正则图关系密切，称为度量方案。此外还有三角形结合方案等其他类型的结合方案。1

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学