[科普中国]-冯·诺伊曼全集

在集合论和有关的数学分支中，冯·诺伊曼全集或冯·诺伊曼集合层次，是由所有集合组成的类，可以分成超限阶级的个体集合（a transfinite hierarchy of individual sets）。

定义冯·诺伊曼全集用超限归纳法定义为如下：

设V0是空集{}。

对于任何序数α，设Vα+1是Vα的幂集。

对于任何极限序数λ，设Vλ是迄今为止所有V-阶段的并集：

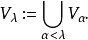
最后，设V是所有V-阶段的并：

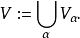等价的说，对于任何序数α，设，这里的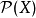是X的幂集。1

V和集合论如果ω是自然数的集合，则Vω是继承有限集合的集合，它是不带有无穷公理的集合论的模型。Vω+ω是普通数学的全集。它是Zermelo集合论的模型。如果κ是不可及基数，则Vκ是Zermelo-Fraenkel集合论自身的模型，而Vκ+1是Morse–Kelley集合论的模型。

注意所有个体阶段Vα都是集合，但是它们的并集V是真类。在V中的集合叫做继承良基集合；基础公理要求所有集合是良基的而因此是继承良基的。（也有的公理系统忽略基础公理，或把基础公理替换为其强否定，如Aczel的反基础公理，不过这类系统很少被用到）。

给定任何集合A，使得A是某个Vα的子集的最小序数α是A的阶（或继承等级）。2

哲学观点有两种不同的方式来理解冯·诺伊曼全集V和ZFC的联系。粗略的说，形式主义者倾向于把V看作是从ZFC公理推出的某种东西（例如，ZFC证明了所有集合都在V中）。在另一方面，实在论者会把冯·诺伊曼全集看作从直觉可直接触及的某种东西，而把ZFC公理看作在V中为真的命题，透过简单论证（透过自然语言），可以使人信服它们的真确性。一个可能的中间立场是，冯·诺伊曼层次的形象化概念给ZFC公理提供了一个动机（所以这些公理不是任意提出来的），但这不意味ZFC公理确实有描述真实存在的对象。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学