[科普中国]-艾礼富数

在集合论中，阿列夫数，又称艾礼富数，是一连串超穷基数。

简介艾礼富数的标记符号为 ℵ （由希伯来字母א‎(aleph)演变而来）加角标表示。

可数集（包括自然数）的势标记为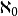 ，下一个较大的势为 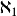，再下一个是 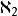，以此类推。一直继续下来，便可以对任一序数 α 定义一个基数 。

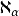这一概念来自于康托尔，他定义了势，并认识到无穷集合是可以有不同的势的。

阿列夫数与一般在代数与微积分中出现的无限(∞) 不同。阿列夫数用来衡量集合的大小，而无限只是在极限的写法中出现，或是定义成扩展的实轴上的端点。某些阿列夫数会大于另一些阿列夫数，而无限只是无限而已。

构造性定义阿列夫数的直观定义并没有解释什么叫“下一个较大的势”，也没有证明是否存在“下一个较大的势”。即便承认对任意的基数都存在更大的基数，是否存在“下一个较大的势”使得这个基数和“下一个较大的基数”之间不再有其他的基数仍然是个问题。下面的构造型定义解决这个问题：

ℵ0定义从前，它是一个良序集ℕ的序数；

考虑良序集按照某种同构关系划出的等价类；

如上定义的等价类有一个特点：可比较，

设ℵa已定义且是一良序集的基数，考虑：

由于ℵa是某良序集的基数，这个良序集必存在于某个等价类中；一定还有其他基数为ℵa的良序集，这些良序集必将也存在于某个等价类中（可能与上面的同属同一个等价类，但不一定）。所有这些等价类将做成一集，记为Z(ℵa)。

Z(ℵa)也是良序集。

定义ℵa+1:= card(Z(ℵa))，它是一个良序集的基数。1

阿列夫是所有可数序数集合的势，称为ω1或有时为Ω。这个ω1本身是一个比所有可数序数更大的序数，因此它为一个不可数集。

在中国大陆，实数集的基数常被记为 c 或 ℵ，即 ℵ := ℶ₁，这样连续统假设就常常被表述为 ℵ = ℵ₁．阅读相关读物时应避免混淆。人们在学数学分析（微积分）时常常以为自己时常遇到的是阿列夫数，事实上他们遇到的是 “ℵ”或“c”，即角标为1的ℶ 数。除非讨论集合论，否则阿列夫数将是最不常用的基数之一。

另见格奥尔格·康托尔

基数

不可数集合

连续统假设

数

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学