在计算机科学中,Hopcroft-Karp算法是一种算法,它将二分图作为输入,并产生最大基数匹配一组尽可能多的边,其特性是没有两条边共享一个端点。
该算法由John Hopcroft和Richard Karp(1973)发现。正如之前的匹配方法,如匈牙利算法和Edmonds(1965)的工作一样,Hopcroft-Karp算法通过寻找增广路径反复增加部分匹配的大小:在进入和离开之间交替的边缘序列。
增加路径在某些部分匹配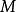 中不是边缘端点的顶点称为自由顶点。算法所依赖的基本概念是增强路径,从自由顶点开始,在自由顶点结束的路径,以及在路径中不匹配和匹配的边之间交替的路径。根据该定义,除了端点之外,扩充路径中的所有其他顶点(如果有的话)必须是非自由顶点。增强路径可以仅由两个顶点(两个都是自由的)和它们之间的单个不匹配边缘组成。
中不是边缘端点的顶点称为自由顶点。算法所依赖的基本概念是增强路径,从自由顶点开始,在自由顶点结束的路径,以及在路径中不匹配和匹配的边之间交替的路径。根据该定义,除了端点之外,扩充路径中的所有其他顶点(如果有的话)必须是非自由顶点。增强路径可以仅由两个顶点(两个都是自由的)和它们之间的单个不匹配边缘组成。
如果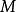 是匹配的,并且
是匹配的,并且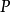 是相对于
是相对于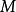 的扩充路径,那么两组边的对称差异,
的扩充路径,那么两组边的对称差异,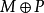 将与大小
将与大小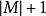 形成匹配因此,通过找到增强路径,算法可以增加匹配的大小。
形成匹配因此,通过找到增强路径,算法可以增加匹配的大小。
相反,假设匹配的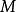 不是最优的,让
不是最优的,让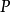 为对称差异
为对称差异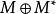 其中
其中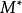 是最佳匹配。因为
是最佳匹配。因为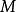 和
和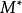 都是匹配,所以每个顶点在
都是匹配,所以每个顶点在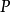 中的度数最多为2。所以
中的度数最多为2。所以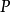 必须形成一个集合不相交周期,
必须形成一个集合不相交周期,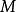 中具有相同数量的匹配和不匹配边的路径,增加
中具有相同数量的匹配和不匹配边的路径,增加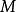 的路径,以及增加
的路径,以及增加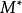 的路径*;但后者是不可能的,因为
的路径*;但后者是不可能的,因为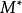 是最优的,具有相同数量的匹配和不匹配顶点的周期和路径不会导致
是最优的,具有相同数量的匹配和不匹配顶点的周期和路径不会导致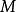 和
和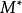 之间的大小差异,因此这个差异等于
之间的大小差异,因此这个差异等于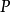 中
中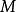 的扩充路径的数量。因此,只要存在匹配的
的扩充路径的数量。因此,只要存在匹配的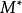 大于当前匹配的
大于当前匹配的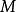 ,还必须存在增强路径。如果没有找到扩充路径,则算法可以安全地终止,因为在这种情况下
,还必须存在增强路径。如果没有找到扩充路径,则算法可以安全地终止,因为在这种情况下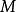 必须是最优的。
必须是最优的。
匹配问题中的增强路径与在最大流动问题中产生的增大路径密切相关,沿着该路径可以增加流动的端子之间的流动量。可以将二分匹配问题转换为最大流动实例,使得匹配问题的交替路径成为增加流动问题的路径。实际上,将Hopcroft-Karp算法中使用的技术推广到任意流网络被称为Dinic算法。
算法该算法可以用以下伪代码表示。
输入:二分图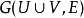
输出:匹配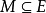
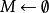
重复
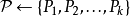 最大的顶点不相交最短增广路径集
最大的顶点不相交最短增广路径集
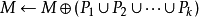
until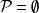
更详细地说,让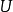 和
和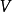 为
为 的两个分区中的两个集合,并让
的两个分区中的两个集合,并让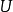 与
与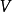 匹配任何时候V都表示为集
匹配任何时候V都表示为集 .算法分阶段运行。每个阶段包括以下步骤。
.算法分阶段运行。每个阶段包括以下步骤。
广度优先搜索将图的顶点划分为多个层。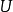 中的自由顶点用作此搜索的起始顶点,并形成分区的第一层。在搜索的第一级,只有不匹配的边,因为
中的自由顶点用作此搜索的起始顶点,并形成分区的第一层。在搜索的第一级,只有不匹配的边,因为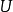 中的自由顶点根据定义不与任何匹配的边相邻。在随后的搜索级别,遍历的边缘需要在匹配和不匹配之间交替。也就是说,当从
中的自由顶点根据定义不与任何匹配的边相邻。在随后的搜索级别,遍历的边缘需要在匹配和不匹配之间交替。也就是说,当从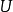 中的顶点搜索后继者时,可以仅遍历不匹配的边,而从
中的顶点搜索后继者时,可以仅遍历不匹配的边,而从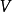 中的顶点可以仅遍历匹配的边。搜索终止于第一层
中的顶点可以仅遍历匹配的边。搜索终止于第一层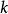 ,其中到达
,其中到达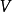 中的一个或多个自由顶点。
中的一个或多个自由顶点。
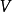 层
层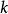 中的所有自由顶点都被收集到一个集
中的所有自由顶点都被收集到一个集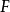 中。也就是说,顶点
中。也就是说,顶点 被放入
被放入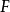 当且仅当它结束最短的增强路径。
当且仅当它结束最短的增强路径。
该算法找到长度为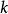 的最大顶点不相交增广路径集。 (最大意味着不能再添加这样的路径。这与找到这样的路径的最大数量是不同的,这将更难做到。幸运的是,这里找到最大路径集就足够了。)这个集合可能是通过深度优先搜索(DFS)从
的最大顶点不相交增广路径集。 (最大意味着不能再添加这样的路径。这与找到这样的路径的最大数量是不同的,这将更难做到。幸运的是,这里找到最大路径集就足够了。)这个集合可能是通过深度优先搜索(DFS)从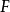 到
到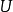 中的自由顶点计算,使用广度第一层来指导搜索:DFS只允许跟随导致未使用的边缘上一层中的顶点,DFS树中的路径必须在匹配和不匹配的边之间交替。一旦找到涉及
中的自由顶点计算,使用广度第一层来指导搜索:DFS只允许跟随导致未使用的边缘上一层中的顶点,DFS树中的路径必须在匹配和不匹配的边之间交替。一旦找到涉及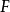 中的一个顶点的扩充路径,DFS将从下一个起始顶点继续。在DFS期间遇到的任何顶点都可以立即标记为已使用,因为如果在DFS的当前点没有从它到
中的一个顶点的扩充路径,DFS将从下一个起始顶点继续。在DFS期间遇到的任何顶点都可以立即标记为已使用,因为如果在DFS的当前点没有从它到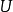 的路径,那么该顶点不能用于到达
的路径,那么该顶点不能用于到达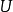 在DFS的任何其他地方。这确保了DFS的
在DFS的任何其他地方。这确保了DFS的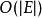 运行时间。也可以在另一个方向上工作,从
运行时间。也可以在另一个方向上工作,从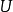 中的自由顶点到
中的自由顶点到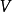 中的自由顶点,这是伪代码中使用的变体。
中的自由顶点,这是伪代码中使用的变体。
以这种方式找到的每条路径都用于放大 .
.
当在其中一个阶段的广度优先搜索部分中找不到更多增强路径时,该算法终止。
分析每个阶段包括单个广度优先搜索和单个深度优先搜索。因此,可以在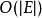 时间内实现单个阶段。因此,在
时间内实现单个阶段。因此,在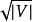 的图形中,第一个
的图形中,第一个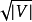 阶段顶点和
阶段顶点和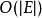 边缘,花费时间
边缘,花费时间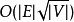 。
。
可以示出每个阶段将最短增强路径的长度增加至少一个:该阶段找到给定长度的最大增强路径集合,因此任何剩余的增强路径必须更长。因此,一旦算法的初始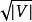 阶段完成,最短的剩余扩充路径至少具有
阶段完成,最短的剩余扩充路径至少具有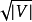 边缘。然而,最终相位和由初始相位找到的部分匹配M的对称差异形成顶点不相交的增广路径和交替循环的集合。如果此集合中的每个路径的长度至少为
边缘。然而,最终相位和由初始相位找到的部分匹配M的对称差异形成顶点不相交的增广路径和交替循环的集合。如果此集合中的每个路径的长度至少为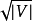 ,则最多可以
,则最多可以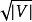 集合中的路径,最佳匹配的大小最多不同于
集合中的路径,最佳匹配的大小最多不同于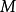 的大小
的大小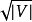 边缘。由于算法的每个阶段都将匹配的大小增加了至少一个,因此在算法终止之前,最多可以有
边缘。由于算法的每个阶段都将匹配的大小增加了至少一个,因此在算法终止之前,最多可以有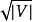 个附加阶段。
个附加阶段。
由于该算法最多执行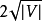 阶段,因此总时间为
阶段,因此总时间为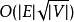 )在最坏的情况下。
)在最坏的情况下。
然而,在许多情况下,算法所花费的时间甚至可能比这种最坏情况分析所指示的更快。例如,在稀疏二分随机图的平均情况下,Bast等。 (2006)(改进了Motwani 1994的先前结果)表明,所有非最优匹配都具有高概率增强的对数长度路径。因此,对于这些图,Hopcroft-Karp算法采用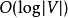 阶段和
阶段和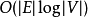 总时间。1
总时间。1
本词条内容贡献者为:
李嘉骞 - 博士 - 同济大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国