[科普中国]-代理损失函数

代理损失函数或者称为替代损失函数，一般是指当目标函数非凸、不连续时，数学性质不好，优化起来比较复杂，这时候需要使用其他的性能较好的函数进行替换。

定义在二元分类问题中，假如我们有n个训练样本{(X1,y1),(X2,y2),⋯,(Xn,yn)}，其中yi∈{0,1}。为了量化一个模型的好坏，我们通常使用一些损失函数，损失函数越小，模型越好。最常用的损失函数就是零一损失函数。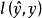

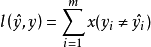对于一损失函数l，目标是要找到一个最优的分类器h，使得这个分类器在测试样本上的期望损失最小。数学式子表达是：

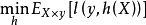理论上，我们是可以直接对上式进行优化，得到最优的分类器h。然而这个过程是非常困难的（甚至不可行）。其一是因为X×y的概率分布是未知的，所以计算loss的期望是不可行的。另外一个难处是这个期望值很难进行优化，因为这个损失函数是非连续的，这个优化问题本质是NP-Hard的。举个例子来说，假定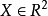，我们希望找一个线性分类器

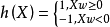使得loss的期望最小化。所以也就是求解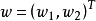。关于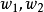以及loss的图像大致如下：

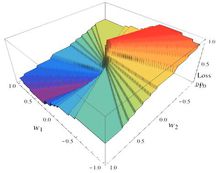
这个函数显然是非连续的。常用的优化方法，比如梯度下降，对此都失效了。正因此，可以考虑一个与零一损失相接近的函数，作为零一损失的替身。这个替身就称作代理损失函数（surrogate loss function）1。

性质如果最优化代理损失函数的同时也最优化了原本的损失函数，就称校对性(calibration)或者一致性(consistency)。这个性质与所选择的代理损失函数相关。一个重要的定理是，如果代理损失函数是凸函数，并且在0点可导，其导数小于0，那么它一定是具有一致性的1。

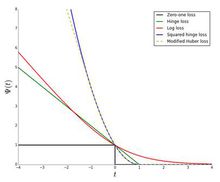
零一损失函数与logloss，hinge loss，squared hinge loss以及modified Huber loss的联系如下图：

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学