热传导方程(或称热方程)是一个重要的偏微分方程,它描述一个区域内的温度如何随时间变化。
简介热传导方程(或称热方程)是一个重要的偏微分方程,它描述一个区域内的温度如何随时间变化。1
物理动机热传导在三维的等方向均匀介质里的传播可用以下方程表达:
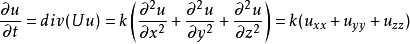 其中:u=u(t,x,y,z)表温度,它是时间变数t与空间变数(x,y,z)的函数;
其中:u=u(t,x,y,z)表温度,它是时间变数t与空间变数(x,y,z)的函数; 是空间中一点的温度对时间的变化率;
是空间中一点的温度对时间的变化率; 与
与 温度对三个空间坐标轴的二次导数;k是热扩散率,决定于材料的热传导率、密度与热容。
温度对三个空间坐标轴的二次导数;k是热扩散率,决定于材料的热传导率、密度与热容。
热方程是傅里叶冷却律的一个推论(详见条目热传导)。如果考虑的介质不是整个空间,则为了得到方程的唯一解,必须指定u的边界条件。如果介质是整个空间,为了得到唯一性,必须假定解的增长速度有个指数型的上界,此假定吻合实验结果。
热方程的解具有将初始温度平滑化的特质,这代表热从高温处向低温处传播。一般而言,许多不同的初始状态会趋向同一个稳态(热平衡)。因此我们很难从现存的热分布反解初始状态,即使对极短的时间间隔也一样。
热方程也是抛物线偏微分方程最简单的例子。利用拉普拉斯算子,热方程可推广为下述形式
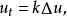 其中的
其中的 是对空间变数的拉普拉斯算子。
是对空间变数的拉普拉斯算子。
热方程支配热传导及其它扩散过程,诸如粒子扩散或神经细胞的动作电势。热方程也可以作为某些金融现象的模型,诸如布莱克-斯科尔斯模型与Ornstein-Uhlenbeck过程。热方程及其非线性的推广型式也被应用于影像分析。量子力学中的薛定谔方程虽然有类似热方程的数学式(但时间参数为纯虚数),本质却不是扩散问题,解的定性行为也完全不同。
就技术上来说,热方程违背狭义相对论,因为它的解表达了一个扰动可以在瞬间传播至空间各处。扰动在前方光锥外的影响通常可忽略不计,但是若要为热传导推出一个合理的速度,则须转而考虑一个双曲线型偏微分方程。1
应用热方程在许多现象的数学模型中出现,而且常在金融数学中作为期权的模型出现。著名的布莱克-斯科尔斯模型中的差分方程可以转成热方程,并从此导出较简单的解。许多简单期权的延伸模型没有解析解,因此必须以数值方法计算模型给出的定价。热方程可以用Crank-Nicolson法有效地求数值解,此方法也可用于许多无解析解的模型。1
参见热
偏微分方程
发展方程
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国