[科普中国]-热量子场论

在理论物理中，热量子场论 (简称热场论) 或有限温度场论 (finite temperature field theory) 是计算在有限 (不为零的) 温度下，量子场论中物理可观察量之期望值的方法。

简介在理论物理中，热量子场论(简称热场论) 或有限温度场论(finite temperature field theory) 是计算在有限 (不为零的)温度下，量子场论中物理可观察量之期望值的方法。

在松原方法(Matsubara formalism) 中，一个运算子在热系综的期望值

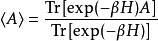
可以被量子场论中以虚数时间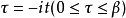所演化的期望值所表示。由于使用虚数时间，计算上可以使用欧几里得度量的时空。式中的迹 要求所有的玻色场在欧几里德时间方向τ上皆有周期为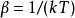的周期性，而费米场则有反周期性。此方法让我们能够使用量子场论中已存在的技巧，如泛函积分和费曼图等，并将其中的时间修改为紧致的欧几里德时间来做计算。同时，正规顺序 (Normal Ordering) 的定义也必须被修改。在动量空间下，这对应于将原本连续的频率，以离散的虚数 (松原) 频率取代。透过德布罗意关系，这对应于离散的热能量频谱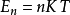。这样的方法被证明对研究量子场论在有限温度下的现象很有效，并且已经被推广到规范场论，是研究杨-米尔斯理论中去禁闭 (deconfining) 相变猜想的重要工具。在欧式空间场论中，实数时间下的可观测量可以由解析延拓获得。

有限温度场论，除了使用非真实的虚数时间来计算，还有两种使用实数时间 (real-time formalism) 的方法。第一种是依路径排序 (path-ordered) 的实数时间方法，其包含了Schwinger-Keldysh formalism及其他更近代的版本。后者将一条原本从负的(大的)初始时间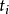出发到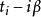的直线路径，取代为一条先经过正的(大的)实数时间 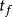再适当的回到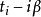的路径。事实上，真正需要的是一段经过实数轴的路段，而前往终点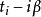所选的路线是较不重要的。这样以区段 (piecewise) 方式组成的复数时间路径，造成场的数量增倍以及更复杂的费曼规则，不过却避免了使用虚数时间方法所需的解析延拓。 另一种实数时间方法称为热场力学 (thermo field dynamics)，是一种以运算子为基础，使用勃格留波夫变换(Bogoliubov transformation) 的方法。就如费曼图和微扰论等方法一样，其他技巧如色散关系 (dispersion relations) 和有限温度的 Cutkosky rules 也都可以在实数时间方法中使用。

另一种在数学物理上感兴趣的方法是使用KMS 态来处理。1

量子场论在理论物理学里，量子场论（英语：Quantum field theory，简称QFT）是结合了经典场论、狭义相对论和量子力学的一套自洽的概念和工具。在粒子物理学和凝聚态物理学中，量子场论可以分别为亚原子粒子和准粒子建立量子力学模型。量子场论将粒子视为更基础的场上的激发态，即所谓的量子，而粒子之间的相互作用则是以相应的场之间的交互项来描述。每个相互作用都可以用费曼图来表示，这些图不但是一种直观视化的方法，而且还是相对论性协变摄动理论中用于计算粒子交互过程的一个重要的数学工具。1

参阅松原频率

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学