[科普中国]-热力学极限

热力学极限是指粒子数（或体积）趋向无穷大时的极限。一般宏观物体包含了10^23个粒子，可以认为是满足热力学极限的。

简介热力学极限是指粒子数（或体积）趋向无穷大时的极限。一般宏观物体包含了1023个粒子，可以认为是满足热力学极限的。1

应用热力学极限是一个统计物理中的常用假设，很多结论只有在热力学极限下才会成立，例如：杨振宁和李政道证明相变只有在热力学极限下才会发生；熵与能量等物理量的广延性只有在热力学极限下才成立。

热力学极限也是玻尔兹曼统计的假设前提之一。1

麦克斯韦-玻尔兹曼统计麦克斯韦—玻尔兹曼统计是描述独立定域粒子体系分布状况的统计规律。

所谓独立定域粒子体系指的是这样一个体系：粒子间相互没有任何作用，互不影响，并且各个不同的粒子之间都是可以互相区别的，在量子力学背景下只有定域分布粒子体系中的粒子是可以相互区分的，因此这种体系被称为独立定域粒子体系。而在经典力学背景下，任何一个粒子的运动都是严格符合力学规律的，有着可确定的运动轨迹可以相互区分，因此所有经典粒子体系都是定域粒子体系，在近独立假设下，都符合麦克斯韦-玻尔兹曼统计。

因而符合麦克斯韦—玻尔兹曼统计分布的粒子，当他们处于某一分布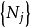（“某一分布”指这样一种状态：即在能量为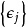的能级上同时有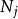个粒子存在着，不难想象，当从宏观观察体系能量一定的时候，从微观角度观察体系可能有很多种不同的分布状态，而且在这些不同的分布状态中，总有一些状态出现的几率特别的大，而其中出现几率最大的分布状态被称为最可几分布）时，体系总状态数为：

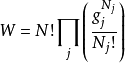
近独立粒子统计力学近独立粒子统计指的是统计力学中对粒子的特定描述，它的特点是不考虑粒子间的相互作用。近独立粒子三种主要模式是：

描述古典系统用：麦克斯韦-玻尔兹曼统计

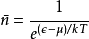
描述含费米子的量子系统用：费米-狄拉克统计

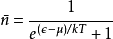
描述含玻色子的量子系统用：玻色-爱因斯坦统计

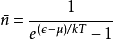
这三种统计的不同之处在于：

在古典物理中，粒子被视为能被区分出来的不同个体。

在量子物理中，两个费米子不能处于同一个物理态。

在量子物理中，要区分玻色子只能从不同的物理态入手，位处同一态的玻色子没有分别。因此，在物理态一的光子甲及在物理态二的光子乙，跟态一的光子甲及在态二的光子乙没有分别。但在古典物理中它们会是两个不同的系统，而在量子物理只算作一个。故玻色子表现得像它们都喜欢在同一状态似的。

数学上使用可交换算符描述玻色子，反交换算符描述费米子，所以造成了以上的差别。1

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学