[科普中国]-重极限

多元实变函数f(p)=f(x1,x2,...,xm )，当它的所有变量同时取极限时函数值的极限，这种极限称为重极限。当自变量x1,x2,...,xm不是同时取极限，而是依一定的顺序相继取极限时，f(x1,x2,...,xm)的极限，称为累次极限。

基本介绍重极限是多元函数的一种极限，因为对n(≥2)元函数而言，极限

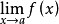中x=(x₁，x₂，…，xn)，a=(a₁，a₂，…，an)∈Rⁿ，x→a意味着同时有x₁→a₁，x₂→a₂，…，xn→an，故称相应的极限为n重极限，作为多元函数特例的多重数列的极限也称为重极限1。如二重极限

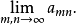
证明重极限不存在常用的方法是证明沿两种不同路径极限不同（通常可取过点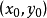的直线）。例如证明重极限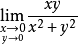不存在，取直线y=kx，让点(x,y)沿直线y=kx趋于（0,0）点此时有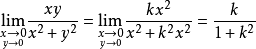，则重极限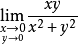不存在2。

求重极限求重极限的常用方法有：

1)利用极限性质(四则运算法则，夹逼原理)；

2)消去分母中极限为零的因子(有理化，等价无穷小代换)；

3)利用无穷小量与有界变量之积为无穷小量2。

【例1】求下列极限

（1）；

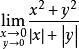解：（1）由于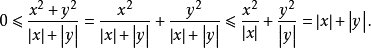

而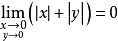，由夹逼原理知.

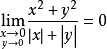（2）.

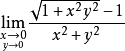解：（2）将分子有理化：

原式=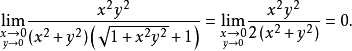

重极限与累次极限的关系多元实变函数f(p)=f(x1,x2,...,xm)，当它的所有变量同时取极限时函数值的极限，这种极限称为重极限。当自变量x1,x2,...,xm不是同时取极限，而是依一定的顺序相继取极限时，f(x1,x2,...,xm)的极限，称为累次极限。

例如，当p(x，y)为平面中的点时，设聚点A的坐标为(a，b)，则f(P)在P→4时的重极限为

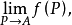我们也把它记作

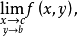而它的两个累次极限则记为

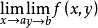与

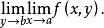
重极限与累次极限的关系

（1）累次极限存在且相等时，重极限未必存在。

（2）重极限存在时，累次极限不一定存在。

（3）若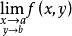与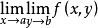都存在，则二者必相等。

（4）若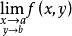与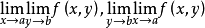都存在，则三者必相等。

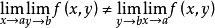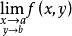（5）若，则不存在。

注意

1.对于二个不同变量的极限过程在交换其次序的时候，应该加以注意，不是无条件地都可以交换次序的。

2.累次极限和重极限的关系也是相当复杂的，不能把重极限存在(或累次极限存在且相等)认为是累次极限相等(或重极限序在)的必要条件3。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学