[科普中国]-风能廓线

风能廓线即风速随高度的变化曲线，以研究大气边界层内的风速规律。

描述及规律在边界层，风速随高度的变化服从普朗特的理论：

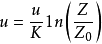
式中u为高度Z上的风速，K为卡曼常数，其值为0.4左右。1n为摩擦速度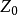，为粗糙度参数。

若换算成两个高度的风速关系，则为：

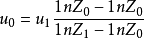
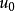为高度Zn的风速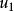，为在高度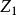处的风速。这是中性平衡时风速随高度变化的对数律公式。在需用速度廓线的许多数学间题中，把对数律公式引进到微分方程中去会发生困难，这时假设混合长度随高度变化为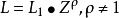，则得到风速随高度变化的乘幂律公式。换成两个高度的风速关系,用以上同样方法可导出公式：

公式中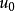、、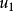Zn、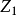含义同上，α为风速随高度变化系数，是一个与大气稳定度和地形条件有关的参数，查表获得，此式通称为指数公式。1

风廓线形状应该指出的是过去的工作中，大气低层风速廓线无论采用指数公式还是对数公式都还是一个统计规律，即这两个公式符合于在长期连续观测取平均值时的风廓线。这种平均风廓线在直角坐标纸上表现为一条风速随高度而增加的曲线，在对数坐标纸上近似为一条直线或接近于直线。但在各次观测中的风速廓线并非都象平均风廓线一样，它可以呈现出各种形状。1

计算方法弄清近地层平均风速垂直分布的规律对于理论研究和实际应用都十分重要。

对数风廓线在中性条件下，对数风速廓线能够很好地描述平均风速随高度的变化。这个关系已经在100m高度以内的实际观测得到了证明。在非中性条件下，必须考虑对稳定度的订正。

复合指数风廓线在不稳定条件和中性条件下，复合指数风速廓线能够较好地描述均匀表面上的近地层风速廓线。这个模式在近来的一些文章中被讨论到，并且有人用实际观测数据进行了检验。

莫宁一奥布霍夫相似理论在非中性条件下，应用莫宁一奥布霍夫相似理论也可以解决稳定度订正的难题，由此建立的通量一廓线关系式已经被成功地应用到近地层风速廓线的描述中。然而，由于必须先通过实验方法确定其中的相似函数，并预先估计奥布霍夫长度和其它一些参数，这使得该方法在估计风速廓线的实际应用中并不方便。2

本词条内容贡献者为:

周敏 - 副教授 - 西南大学