[科普中国]-特徵标理论

在数学里，尤其是在群表示理论里，一个群表示的特征标（character）是指一个将群的每个元素连结至表示空间这个域内的每个元素之函数。特征标蕴藏着群的许多重要性质，且因此可以用来做群的研究。

特征标理论是对有限简单群分类的一个有重要的工具。在范特-汤普逊定理证明接近一半的地方会有一个用到特征标的复杂计算。另外还有一些较简单但一样重要的结论需用在特征标理论，如伯恩赛德定理及理查·布劳尔和铃木通夫所证出之定理，此定理表示有限简单群不会有一个为广义四元群的西洛2-子群。

定义设V为一个域F上的有限维向量空间且设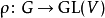 为一个群G于V上的表示。则ρ的特征标即为如下给定之函数

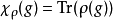
其中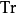 为矩阵的迹数。

一个特征标χρ若被称为是不可约的，即表示ρ是一个不可约表示。若被称为是线性的1，则表示ρ的维度等于1。χρ的核为集合

其中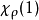 是χρ在群单位元上的值。当ρ是G的k维表示且1为G的单位元时，

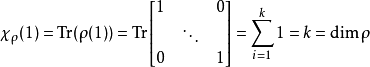
和特征标群的情况不同，一个群的特征标通常不会自己“形成”一个群。

拓扑群的情形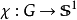 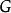在调和分析中，通常定义局部紧阿贝尔拓扑群的特征标为连续群同态；在此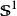， 表示单位圆构成的群，等价地说就是 。

部分作者将特征标的定义放宽为连续群同态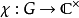 ，而将取值在 者称作么特征标。其他人则保留原初定义，而将这类广义的特征标称为拟特征标。

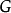的全体特征标构成一个群 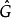，群二元运算的定义是 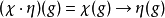，称为对偶群。庞特里雅金对偶性总结了对偶群的一般性质2。

性质特征标是一个类函数，即为对一个共轭类内的所有元素来说，χ会是个常数。

两个同构的表示会有相同的特征标。若系数域的特征char(F)=0，则两个表示为同构的，当且仅当它们有着完全相同的特征标。

若一个表示可以是多个子表示的直和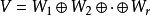： ，则其相对应的特征标会是其所有子表示的特征标之和： 。

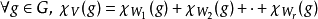在有限群的情况下，每个特征标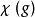 都是n个m次单位根之和，其中n为表示内域的维度，m则是g的阶。

若F是代数封闭的且char(F)不可以整除G的阶|，则G的不可约特征标之数量等于G的共轭类数： 。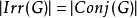

算术性质令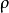 和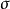 为G的两个表示，则有下列的等式成立：

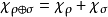
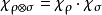
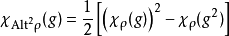
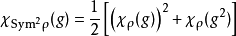
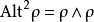其中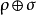 为两者的直和、 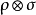为两者的张量积、 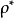为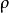 的共轭转置、以及Alt称为交替积而Sym则称为对称方，其值由下式决定

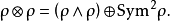
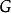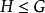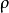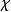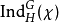特征标的诱导与限制设 为有限群， 为其子群，而 为 G 的表示，其特征标记为 。令 为诱导表示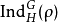 的特征标；根据弗罗贝尼乌斯互反定理，对所有 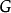的特征标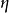 ，恒有下述等式

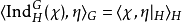此等式可用来刻划类函数 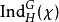。事实上，若选定陪集分解

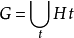还可以明确地写下 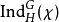的取值：

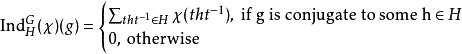特征标表[编辑]

一个有限群的不可约特征标可以形成一个特征标表，其蕴含着许多有关群G在紧致形式时的有用资讯。每一行标记着一个不可约特征标且包含着此一特征标在每个G的共轭类上的值。

下面是有三个元素之循环群C3的特征标表：

|| ||

其中的u为一个原三次单位根。

特征标表总会是正方的，因为不可约表示的数目总会相等于共轭类的数目。特征标表的第一个行总会是1，其对应至群的当然表示上。

正交关系有关特征标表最重要的性质之一为其在行与列上都会有着正交关系。

对特征标(即对特征标表中的行)的内积由下给出：

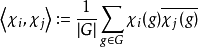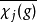其中 表示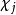 在g上的值的复数共轭。

对于此一内积而言，不可约特征标两两正规正交：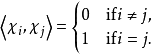

对表中的列的正交关系则由下列给出：

对 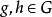，其和为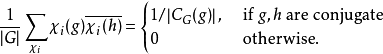

其中相加的范围为所有G的不可约特征标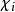，而符号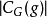则表示为g的共轭类之大小。

此一正交关系可以帮助许多的运算，如：

将一个未知特征标分解成不可约特征标的线性组合。

当只有一些不可约特征标为可知时，建构其完整的特征标表。

求出群的共轭类的表示的中心化子的阶。

求出群的阶。

特征标表性质一个群G的某些性质可以由其特征表中推导出来：

G的阶就是表上所有特征标之在1上的取值的平方：(χ(1))的总和（伯恩赛德公式）。

G是可换的当且仅当对每个在表上的特征标，χ(1) = 1。

G有一个非当然正规子群(即G不是一个简单群)当且仅当对于某些表上的非当然特征标χ和一些于G内的非单位元素g，会有χ(1) = χ(g)。

特征标表通常不会将群分至同构：例如，四元群Q和有8个元素的二面体群D4会有同样的特征标表。

对有限群之特别例子，详见有限群表示理论。

一维表示的特征标会形成一个特征标群，其和数论中有着很重要的关连

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学