赫尔维茨ζ函数(Hurwitz zeta function)是满足某一形式的函数。此函数可以扩展到 s≠1的亚纯函数。
定义赫尔维茨ζ函数(Hurwitz zeta function)定义如下
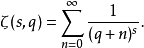 其中q、s都是复数,并且有Re(q)>0,Re(s)>0。
其中q、s都是复数,并且有Re(q)>0,Re(s)>0。
对于给定的q,s,此函数可以扩展到s≠1的亚纯函数。
级数展开赫尔维茨ζ函数可以展开成级数:1
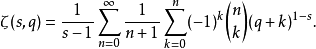 此级数在S空间的紧空间子集中均匀收敛成为一个整函数。
此级数在S空间的紧空间子集中均匀收敛成为一个整函数。
积分式赫尔维茨ζ函数可以表示为下列梅林变换
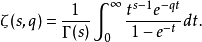 其中Re s>1 及Re q>0。
其中Re s>1 及Re q>0。
赫尔维茨公式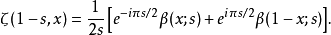 其中
其中
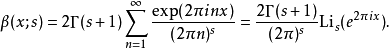 对于
对于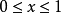 和s>1成立,其中
和s>1成立,其中 代表多重对数。
代表多重对数。
泰勒展开赫尔维茨ζ函数的导数是平移:
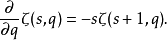 因此赫尔维茨ζ函数的泰勒级数可表示为:
因此赫尔维茨ζ函数的泰勒级数可表示为:
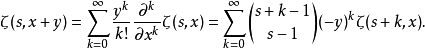 或
或
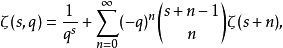 其中 |q|
其中 |q|




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国