[科普中国]-数学三维投影

数学三维投影是将三维空间中的点映射到二维平面上的方法。由于目前绝大多数图形数据的显示方式仍是二维的，因此三维投影的应用相当广泛，尤其是在计算机图形学，工程学和工程制图中。

分类三维图形平面投影

平行投影：投影中心与投影平面的距离是无限的，投影线相互平行

正投影（正交投影）：投影线垂直于投影平面

多视图投影：物体的坐标面与投影面平行，正视图、侧视图、俯视图

轴测投影：物体的三个坐标面或坐标轴与投影面均不平行

正等轴测投影（正等测）：投影时三个坐标轴等比例缩放，投影面坐标轴夹角120°

正二轴测投影（正二测）：投影时两个坐标轴等比例缩放，第三个坐标轴缩放比例不同

正三轴测投影（正三测）：投影时三个坐标轴缩放比例均不相等

斜投影：投影线不垂直于投影平面

斜等轴测投影（斜等测）

斜二轴测投影（斜二测）

斜三轴测投影（斜三测）

透视投影：投影中心与投影平面的距离是有限的

一点透视

两点透视

三点透视

平行投影平行投影是投影线相互平行的投影。若投影线平行于投影面则称正投影，若投影面倾斜于投影面则称斜投影。

正交投影正交投影是一系列用于显示三维物体的轮廓、细节或精确测量结果的变换方法。通常又称作截面图、鸟瞰图或立面图。

当视平面的法向（即摄像机的朝向）平行于笛卡尔坐标系三根坐标轴中的一根，数学变换定义如下： 若使用一个平行于y轴（侧视图）的正交投影将三维点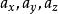 投影到二维平面上得到二维点 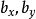，可以使用如下公式

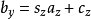
其中向量s是一个任意的缩放因子，而c是一个任意的偏移量。这些常量可自由选择，通常用于将视口调整到一个合适的位置。该投影变换同样可以使用矩阵表示（为清晰起见引入临时向量d）

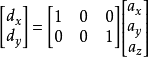
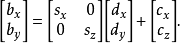
虽然正交投影产生的图像在一定程度上反映了物体的三维特性，但此类投影图像和实际观测到的并不相同。特别是对于相同长度的平行线段，无论离虚拟观察者（摄像机）远近与否，它们都会在正交投影中显示为相同长度。这会导致较近的线段看起来被缩短了。1

斜投影斜投影不像正交投影一样投影线垂直于投影面，而是投影线与投影面成非90度的斜角。2

透视投影透视投影的定义更为复杂。可以将其理解为透过摄像机取景器对于被投影物体进行观察。摄像机的位置、朝向和视野都将影响投影变换的结果。我们定义以下变量来对这一变换进行描述：

1、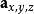：将被投影的三维空间中的点。

2、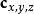：摄像机的位置。

3、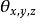：摄像机的旋转角度。当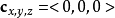且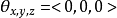, 三维向量将被投影到二维向量。

4、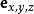：观测者相对显示平面的位置。

最终结果为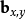：：所产生的二维投影。

首先我们定义点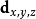作为点 {\displaystyle \mathbf {a} } \mathbf {a} 向摄像机坐标系所作的变换，其中摄像机坐标系由摄像机的位置c和旋转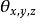所决定。该过程为：先用a减去c，然后使用由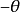产生的旋转矩阵乘上该结果。该变换通常称为摄像机变换(注意该计算过程假设使用左手法则)：

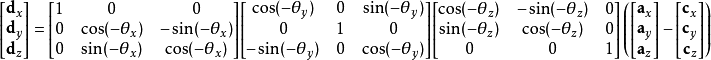或者使用以下这种非矩阵表示的形式，其中角度的正负号与矩阵表示形式不同：

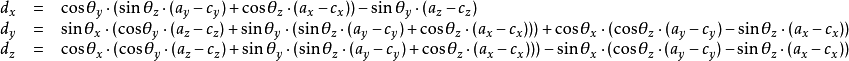然后将变换后的该点通过以下方程投影到二维平面（此处投影平面为x/y平面，有时也使用x/z）:

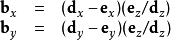或在齐次坐标系下可以表示为：

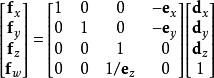和

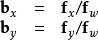
观测者到显示平面的距离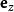，，直接关系到视野的大小。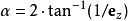为可视角度。（这里假设屏幕的两角为(-1,-1)和(1,1)）

如果要在一些特定的显示设备上显示该二维平面，之后还要进行一些必要的剪裁和缩放操作。3

图示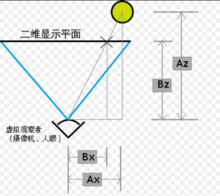

计算三维空间中位于Ax，Az的点在屏幕坐标x轴的位置：

对于y轴同样有:

(其中Ax和Ay是透视转换前物体在空间中的坐标)4

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学