数学上,贝西科维奇(Besicovitch)覆盖定理是实分析的一条覆盖定理。欧氏空间的任何一个有半径上限的闭球族中,可以取出几个子集,子集的球互不相交,且覆盖原来闭球族中所有球的中心,而子集的数目上限只取决于空间的维数。
定理叙述若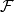 是
是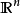 中的非退化(半径为正数)闭球族,当中的球的半径有有限上界,即1
中的非退化(半径为正数)闭球族,当中的球的半径有有限上界,即1
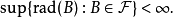
而A为当中的球的中心组成的集合。那么F中存在子集 ,每个
,每个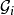 是可数多个互不相交的球的集合,而且
是可数多个互不相交的球的集合,而且
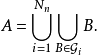 其中
其中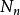 是一个仅依赖于n的常数。
是一个仅依赖于n的常数。
证明先假设A是有界集合。依次选取球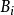 ,选择
,选择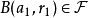 为
为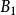 ,适合条件
,适合条件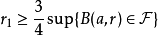 。
。
若已选取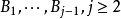 。令
。令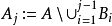 。若
。若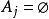 ,就停止;若否,选择
,就停止;若否,选择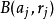 为Bj,适合条件
为Bj,适合条件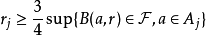 。
。
球 Bi有以下性质:
(1)以Bi的选取方法可知,若j>i,则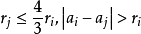 。
。
(2)将全部球Bi的半径缩至三分之一,从以上不等式,可证这些缩小的球 互不相交。
互不相交。
(3)若有可数无限多球Bi,因A有界,及缩小的球不交的性质,所以球Bi的半径趋向0。
(4)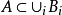 。若Bi数目有限,则结果明显;若数目是无限多,假如有
。若Bi数目有限,则结果明显;若数目是无限多,假如有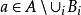 ,那么F中有球B(a,r),而从上一性质知,对足够大的j,有
,那么F中有球B(a,r),而从上一性质知,对足够大的j,有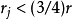 ,与Bj的选取条件矛盾。
,与Bj的选取条件矛盾。
对k> 1,估算Bk和多少个之前选择的球Bi相交。先将这样的Bi按半径ri分成两组: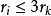 为第一组,
为第一组,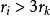 为第二组。
为第二组。
对第一组的球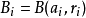 ,将其缩小成
,将其缩小成 后包含在
后包含在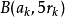 中。
中。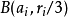 之间互不相交,故总体积不超过
之间互不相交,故总体积不超过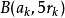 的体积。又因
的体积。又因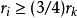 ,因此
,因此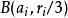 相对
相对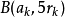 的比例有一个下限,而这下限仅由维数n决定。所以第一组的球的数目有一个仅依赖于n的上限。
的比例有一个下限,而这下限仅由维数n决定。所以第一组的球的数目有一个仅依赖于n的上限。
对第二组的球,任取其中两个球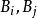 。考虑以
。考虑以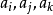 作顶点的三角形。因Bi,Bj都和Bk相交,又ak不在
作顶点的三角形。因Bi,Bj都和Bk相交,又ak不在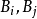 之内,故有不等式
之内,故有不等式
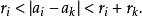
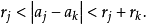 继而证出此三角形以ak为顶点的角
继而证出此三角形以ak为顶点的角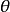 ,不小于一常数。
,不小于一常数。
将第二组各个的球的中心和ak之间连成直线,则任意两条直线之间在ak的夹角不小于arccos(61/64)。ak为中心的单位球面上,这些直线中任何两条和球面的交点,其间的球面距离,等于直线间的夹角。直线间的夹角下限,就是交点间的球面距离下限。在单位球面上所能容纳的这样的点的数目,有一个只依赖维数n的上限,这也就是第二组球的数目上限。
Bk和之前的球相交的数目上限,是以上两组的上限的和,于是这个上限只依赖于维数n。这个上限加1设为Mn。现在从 B1开始依次把球放到子集Gi内。轮到Bk时,因为之前的球中最多有Mn-1个和Bk相交,因此在Mn个子集Gi中,必定有至少一个所包含的球都不和Bk相交,于是可以把Bk加进这个子集。这样就得出了子集Gi,满足条件
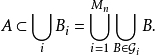 对一般的A,设
对一般的A,设
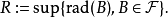 对每个正整数l,设
对每个正整数l,设
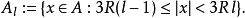
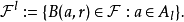 将以上结果用到
将以上结果用到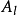 和
和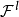 上,得到子集
上,得到子集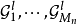 ,满足条件
,满足条件
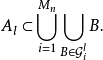 对
对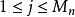 ,设
,设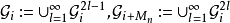 ,并设
,并设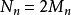 。那么
。那么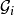 的球互不相交,且有
的球互不相交,且有
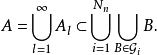 因此定理得证。
因此定理得证。
参见维塔利覆盖引理
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国